Umgekehrt proportionale Funktion

Eine Funktion ist umgekehrt proportional, wenn Folgendes gilt:

 

$$ y \cdot x=k $$

 

Das bedeutet, dass wenn man die beiden Koordinaten x und y miteinander multipliziert, jedes Koordinatenpaar dasselbe Ergebnis (k) liefert.

 

Zum Beispiel die folgenden Koordinatenpaare:

 

$$ (1,20) = 1 \cdot 20 = 20 $$

$$ (2,10) = 2 \cdot 10 = 20 $$

$$ (4,5) = 4 \cdot 5 = 20 $$

$$ (5,4) = 5 \cdot 4 = 20 $$

$$ (10,2) = 10 \cdot 2 = 20 $$

$$ (20,1) = 20 \cdot 1 = 20 $$

 

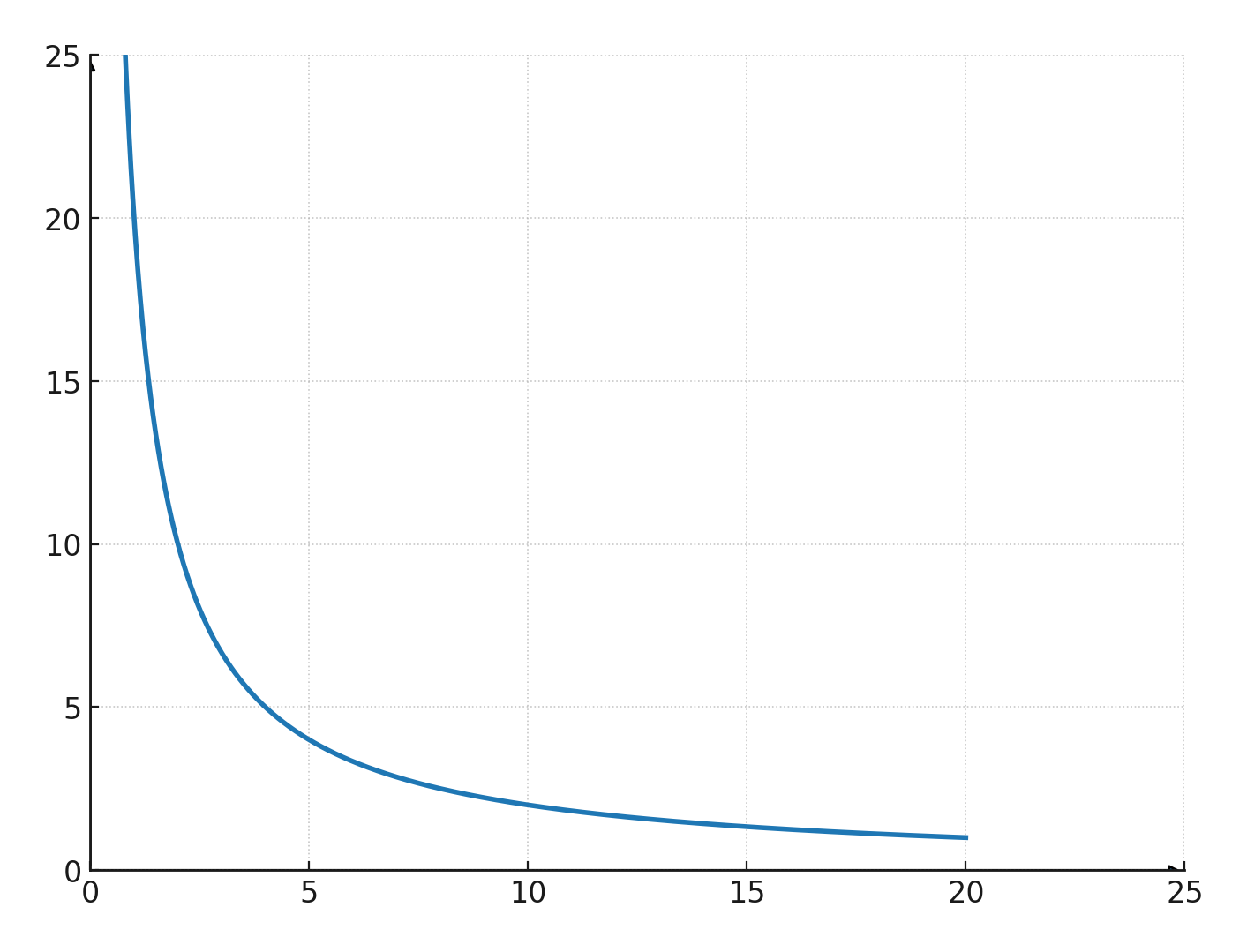
Trägt man diese Koordinatenpaare in ein Koordinatensystem ein, erhält man die untenstehende Kurve, die immer Asymptoten entlang beider Achsen hat.

Das bedeutet, dass sie sich den Achsen sehr stark annähern kann, sie aber niemals schneidet.

 

 

Die Konstante k

k wird als Proportionalitätskonstante bezeichnet.

Die Funktionsgleichung der umgekehrten Proportionalität schreibt man so:

 

$$ f_{(x)} = \frac{k}{x} $$

 

\( x \) darf nicht 0 sein. Man kann nicht durch 0 teilen.

Wenn die Konstante 15 beträgt und x = 5 ist, dann gilt y = 3

 

$$ y = \frac{15}{5} $$

$$ y = 3 $$

 

Auf diese Weise kannst du weitere Koordinatenpaare mit derselben Konstante (15) berechnen.

Beachte: Wenn du den Punkt \((5,3)\) gefunden hast, gilt auch \((3,5)\).

 

Du kannst es auch mit x = -5 machen, dann ergibt sich y = -3

 

$$ y = \frac{15}{-5} $$

$$ y = -3 $$

 

Wenn du negative Zahlen verwendest, erhältst du eine weitere Kurve, die ein Spiegelbild der ersten ist.

Diese Kurven nennt man eine Hyperbel.

 

Hyperbel

Unten ist eine Hyperbel mit der Konstante 15 dargestellt

Die Koordinaten der Kurve im 1. Quadranten sind in der Wertetabelle eingetragen:

 

\(\Large x \)	1	2	3	5	6	10	15
\(\Large y \)	15	7,5	5	3	2,5	1,5	1

 

 

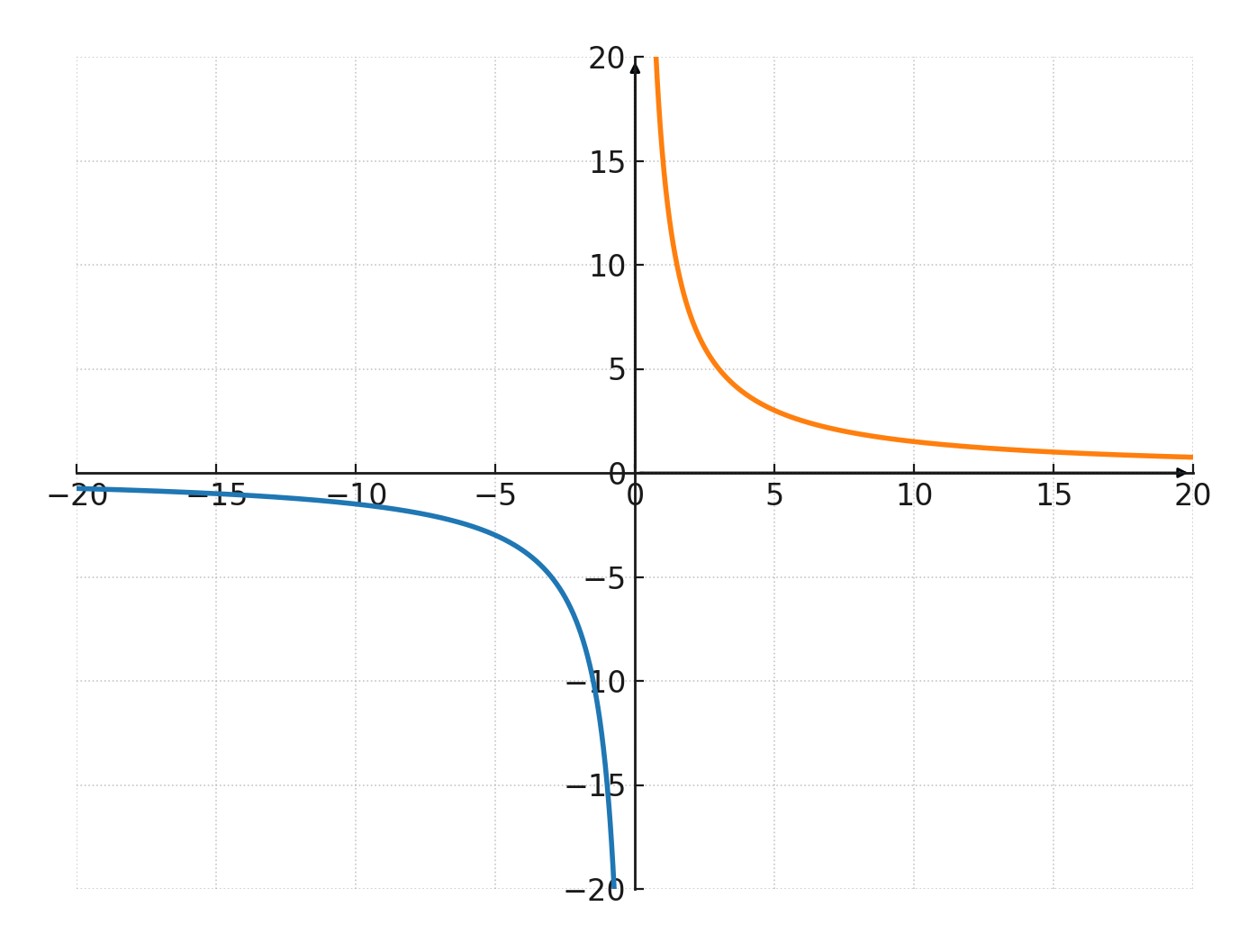
Für die Kurve im 3. Quadranten gilt ebenfalls \( x \cdot y = 15\)

 

\(\Large x \)	-1	-2	-3	-5	-6	-10	-15
\(\Large y \)	-15	-7,5	-5	-3	-2,5	-1,5	-1

 

In diesem Beispiel wurden einige Koordinaten aus Platzgründen weggelassen. Du solltest Koordinatenpaare für alle x von 1 bis 15 berechnen.

So kannst du eine genauere Kurve zeichnen.