Unregelmäßiges Dreieck
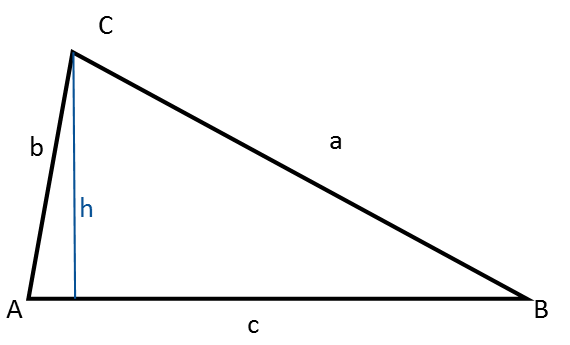
Ein ungleichseitiges Dreieck ist ein Dreieck, bei dem alle Seiten und Winkel unterschiedlich sind, also weder rechtwinklig, gleichschenklig noch gleichseitig.
Formeln und Methoden
Zur Berechnung ungleichseitiger Dreiecke verwendet man den Kosinus- und den Sinussatz.
Beachte, dass bei der Anwendung des Sinussatzes Mehrdeutigkeiten auftreten können, in manchen Fällen gibt es zwei mögliche Dreiecke, die zu den gegebenen Angaben passen und somit zwei Lösungen.
Weitere Informationen zu Kosinus- und Sinussatz findest du unter Trigonometrie.
Um ein ungleichseitiges Dreieck berechnen zu können, muss man eine Seitenlänge und mindestens zwei weitere Angaben über das Dreieck kennen.
In manchen Fällen kann die Höhe des Dreiecks anstelle einer Seitenlänge in den Berechnungen verwendet werden.
Beachte, dass die Höhe das Dreieck in zwei rechtwinklige Dreiecke unterteilt. Das kann bei bestimmten Berechnungen hilfreich sein, da man so die Trigonometrie rechtwinkliger Dreiecke und den Satz des Pythagoras anwenden kann.
Aber DENKE DARAN: Du darfst die Formeln für rechtwinklige Dreiecke nur verwenden, wenn das Dreieck tatsächlich rechtwinklig ist!
Sie dürfen nur verwendet werden, wenn du das Dreieck in zwei rechtwinklige Dreiecke unterteilt hast und mit diesen arbeitest.
Rechts findest du alle Formeln zur Berechnung ungleichseitiger Dreiecke.