Dreiecke
Das erste Polygon.
In der ebenen Geometrie ist das Dreieck das erste Polygon. Es ist die Figur mit den wenigsten Kanten.
Die Grundelemente des Dreiecks
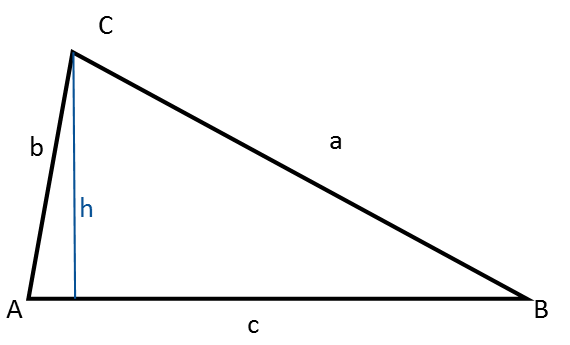
Ein Dreieck hat:
- Drei Winkel, die immer mit Großbuchstaben bezeichnet werden: A, B, C
- Drei Seiten, die immer mit Kleinbuchstaben bezeichnet werden: a, b, c
- Eine Winkelsumme von 180°
Die Höhe in einem Dreieck
Die Höhe in einem Dreieck ist eine Linie, die senkrecht von einer Ecke auf die gegenüberliegende Seite (Grundlinie) fällt.
Ein Dreieck hat drei Höhen, je eine für jede Seite, je nachdem, welche als Grundlinie gewählt wird.
Arten von Dreiecken
Nicht alle Dreiecke sind gleich, daher sind manche auch einfacher zu berechnen als andere.
Dreiecke werden nach ihren Seiten und Winkeln in verschiedene Typen eingeteilt.
Nach Winkeln:
- Wenn einer der Winkel 90° beträgt, nennen wir es ein Rechtwinkliges Dreieck
- Wenn einer der Winkel größer als 90° ist, nennen wir es ein Stumpfwinkliges Dreieck
- Wenn alle Winkel kleiner als 90° sind, nennen wir es ein Spitzwinkliges Dreieck
Nach Seiten:
- Wenn zwei Seiten gleich lang sind, nennen wir es ein Gleichschenkliges Dreieck
- Wenn alle drei Seiten gleich lang sind, nennen wir es ein Gleichseitiges Dreieck
Das Dreieck, das du in der obigen Abbildung siehst, wird ein Allgemeines Dreieck genannt.
- Es hat keinen Winkel von 90°
- Es hat keine gleich langen Seiten.
- Alle Winkel sind jedoch kleiner als 90°, daher ist es auch ein Spitzwinkliges Dreieck.
Ein Dreieck kann nämlich mehrere Eigenschaften gleichzeitig haben. Es kann zum Beispiel sowohl rechtwinklig als auch gleichschenklig sein.
Berechnung von Dreiecken
Menschen berechnen Dreiecke seit Tausenden von Jahren.
Schon die alten Griechen beschäftigten sich mit Geometrie lange vor unserer Zeitrechnung.
Einer der bekanntesten war Pythagoras, der den Satz des Pythagoras formulierte, eine Methode zur Berechnung der Seiten in einem rechtwinkligen Dreieck.
Später entstand die Trigonometrie – ein Teilgebiet der Mathematik, das es ermöglicht, Winkel und Seiten in allen Arten von Dreiecken zu berechnen.
Die Trigonometrie wurde ursprünglich von griechischen Astronomen entwickelt, später aber von Mathematikern weltweit weiterentwickelt und wird heute in Bereichen wie Architektur und Raumfahrt eingesetzt.