Gleichseitiges Dreieck

In einem gleichseitigen Dreieck sind alle drei Seiten gleich lang.

Daher sind auch alle Winkel immer gleich groß.

Bild eines gleichseitigen Dreiecks

Die Winkelsumme in einem Dreieck beträgt immer 180^o. Daher ist es möglich, den Winkel zu berechnen, ohne sonst etwas über das Dreieck zu wissen.

Man muss nur 180 durch 3 teilen:

$$ \frac{180^\circ}{3}=60^\circ $$

Die Winkel in einem gleichseitigen Dreieck sind immer 60 Grad.

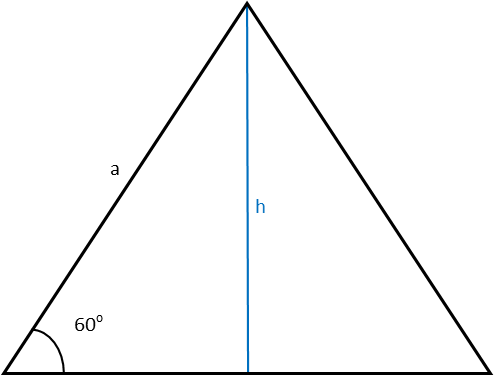
Kennt man entweder die Höhe oder eine Seitenlänge, kann man den Rest des Dreiecks berechnen.

Die Höhe teilt das Dreieck in zwei gleich große rechtwinklige Dreiecke, sodass man Formeln für rechtwinklige Dreiecke verwenden kann.

Rechner

$$ a=\frac{P}{3} $$

$$ a=\frac{h}{sin(60)} $$

$$ a=2\cdot \frac{Area}{h} $$

$$ h = cos(30)\cdot a $$

$$ h=sin(60)\cdot a $$

$$ h = \frac{\sqrt{3}}{2} \cdot a $$

$$ h=\sqrt{a^2- \biggl( \frac{a}{2}\biggr)^2} $$

$$ h= \frac{2\cdot Area}{a} $$

$$ A=\frac{h\cdot a}{2} $$

$$ A=\frac{\sqrt{3}}{4}\cdot a^2 $$

$$ A= \frac{1}{2} \cdot \sqrt{a^4 - \biggl( \frac{a^2}{2}\biggr)^2} $$

$$ P=3\cdot a $$

$$ P= 3\cdot \frac{h}{sin(60)} $$