Funciones fraccionarias
Una función fraccionaria es un sinónimo de una función racional.
Es decir, una función escrita como:
\( \large f(x) = \frac{P(x)}{Q(x)} \)
Al analizar una función fraccionaria, normalmente se procede en este orden:
Primero se encuentra el dominio, luego los ceros, después la intersección con el eje y y, por último, las asíntotas.
Esto da una descripción coherente de la gráfica.
Dominio:
El dominio es el conjunto de todos los valores de x permitidos para la función.
Para una función fraccionaria, el dominio son todos los x reales donde \(\large Q(x)\neq 0 \).
Si tanto numerador como denominador son 0 en el mismo x (factor común), el punto aún se excluye del dominio y se ve como un hueco en la gráfica.
Si \(\large Q(x)=0 \) pero \(\large P(x)\neq 0 \), normalmente se obtiene una asíntota vertical.
Ceros:
La gráfica tiene ceros en los puntos donde el numerador es 0, siempre que el denominador no sea también 0 en el mismo punto.
Intersección con el eje y:
Se encuentra insertando \( \large x = 0 \), si esto está dentro del dominio.
Asíntotas:
Las asíntotas verticales ocurren típicamente en los valores de \( \large x \) donde el denominador es 0. Las asíntotas horizontales u oblicuas se encuentran comparando los grados del numerador y del denominador o mediante la división de polinomios.
Un ejemplo es la función:
$$ \large f(x) = \frac{x^2 - 1}{x^2 - 4} $$
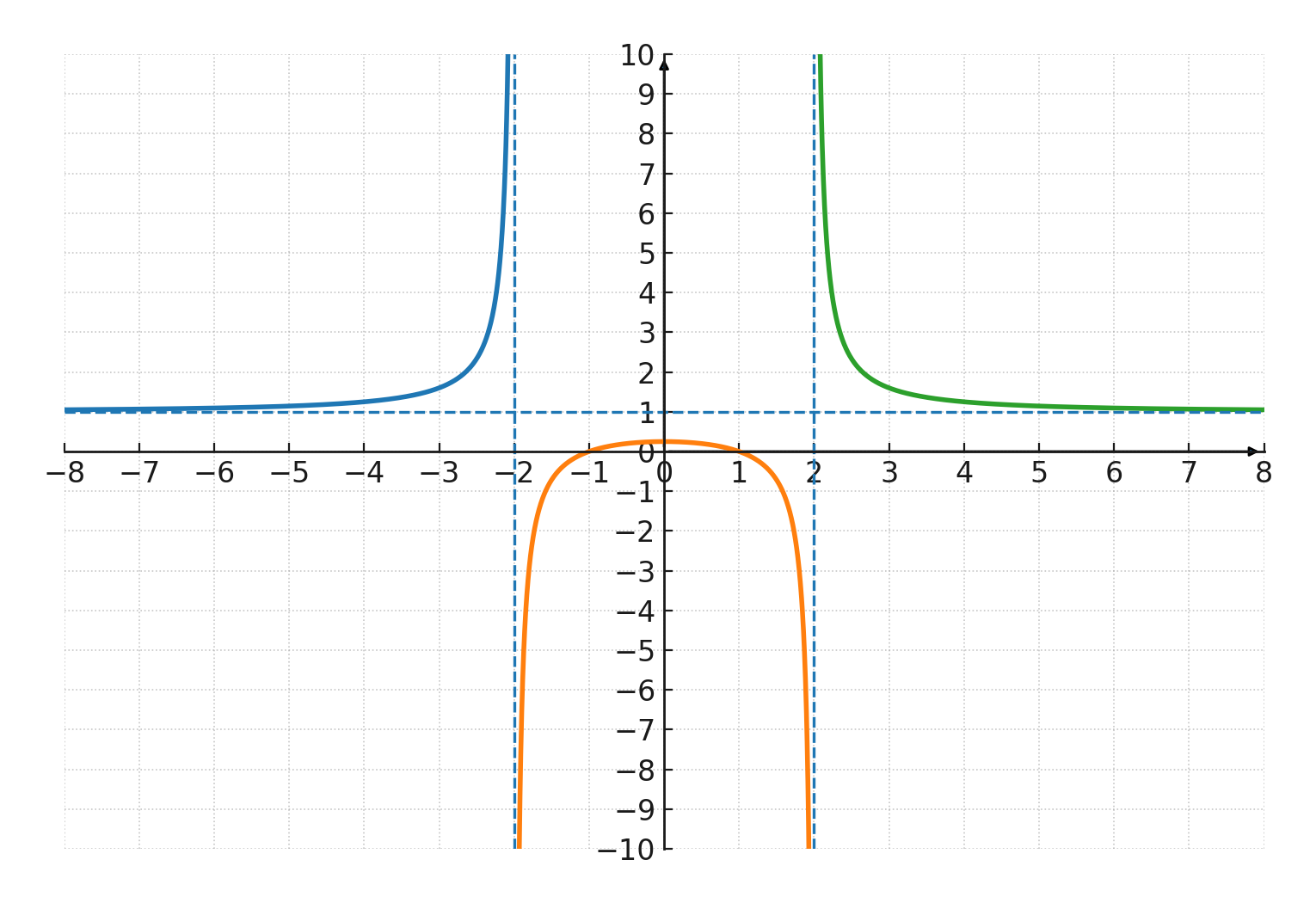
Aquí el numerador es \( \large x^2 - 1 \), lo que da ceros en \( \large x = 1 \) y \( \large x = -1 \).
El denominador \( \large x^2 - 4 \) se hace 0 en \( \large x = -2 \) y \( \large x = 2 \), por lo que la función no está definida allí.
El dominio es, por lo tanto, todos los \( \large x \) reales excepto \( \large -2 \) y \( \large 2 \). La gráfica tiene asíntotas verticales en \( \large x = -2 \) y \( \large x = 2 \).
Como el grado del numerador y del denominador es el mismo, se obtiene una asíntota horizontal en \( \large y = 1 \). La intersección con el eje y se encuentra en \( \large x = 0 \): \( \large f(0) = \frac{-1}{-4} = \frac{1}{4} \).
Con este procedimiento, se obtiene una visión general del comportamiento de las funciones fraccionarias.