Funciones racionales

Una función racional es una fracción donde tanto el numerador como el denominador son polinomios. Así, una función racional se puede escribir como:

 

$$ \large f(x) = \frac{P(x)}{Q(x)} $$

 

Aquí, \(P(x)\) y \(Q(x)\) son polinomios, y el denominador \(Q(x)\) no debe ser igual a 0.

Las funciones racionales pueden tener asíntotas verticales donde el denominador se hace 0, y pueden tener asíntotas horizontales u oblicuas, dependiendo del grado del numerador y del denominador.

 

Ejemplo de una función racional

Un ejemplo de una función racional es:

 

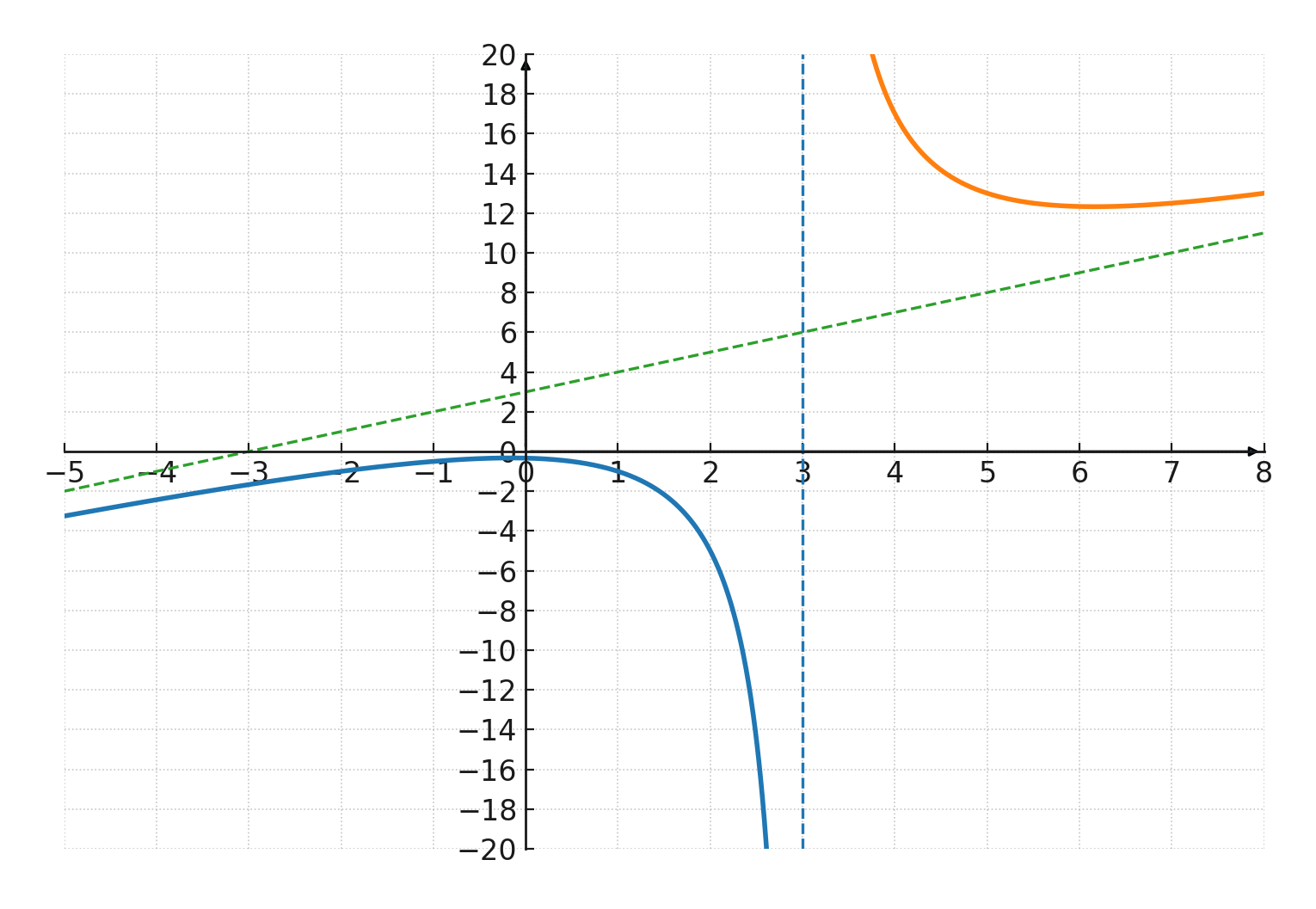
$$ \large f(x) = \frac{x^2+1}{x-3} $$

 

En este ejemplo, el numerador es \(x^2+1\), que es un polinomio de 2º grado, y el denominador es \(x-3\), que es un polinomio de 1º grado.

 

• La función no está definida para \(x=3\), porque no se puede dividir por 0.
• La gráfica tiene por lo tanto una asíntota vertical en \(x=3\).
• Cuando \(x\) se hace muy grande o muy pequeño, la fracción se comporta aproximadamente como \(\tfrac{x^2}{x} = x\). Por lo tanto, la gráfica tiene una asíntota oblicua cerca de la recta \(y=x\).

 

 

 

Proporcionalidad inversa

Uno de los tipos más simples de funciones racionales es la función proporcional inversa:

 

$$ \large f(x) = \frac{k}{x} $$

 

Aquí, \(k\) es una constante. La función no está definida para \(x=0\), porque no se puede dividir por cero.

La gráfica tiene una forma característica, situada en el 1º y 3º cuadrante si \(k\) es positivo, y en el 2º y 4º cuadrante si \(k\) es negativo.

 

Esta función se llama proporcional inversa porque cuando \(x\) se duplica, \(f(x)\) se reduce a la mitad. El producto \(x \cdot f(x)\) siempre es el mismo (igual a \(k\)).