Asíntotas

Una asíntota es una línea a la que la gráfica de una función se acerca cada vez más, sin llegar nunca a cortarla (o solo en puntos aislados). Para las funciones racionales, las asíntotas son muy comunes.

 

Existen tres tipos de asíntotas:

 

Asíntotas verticales:

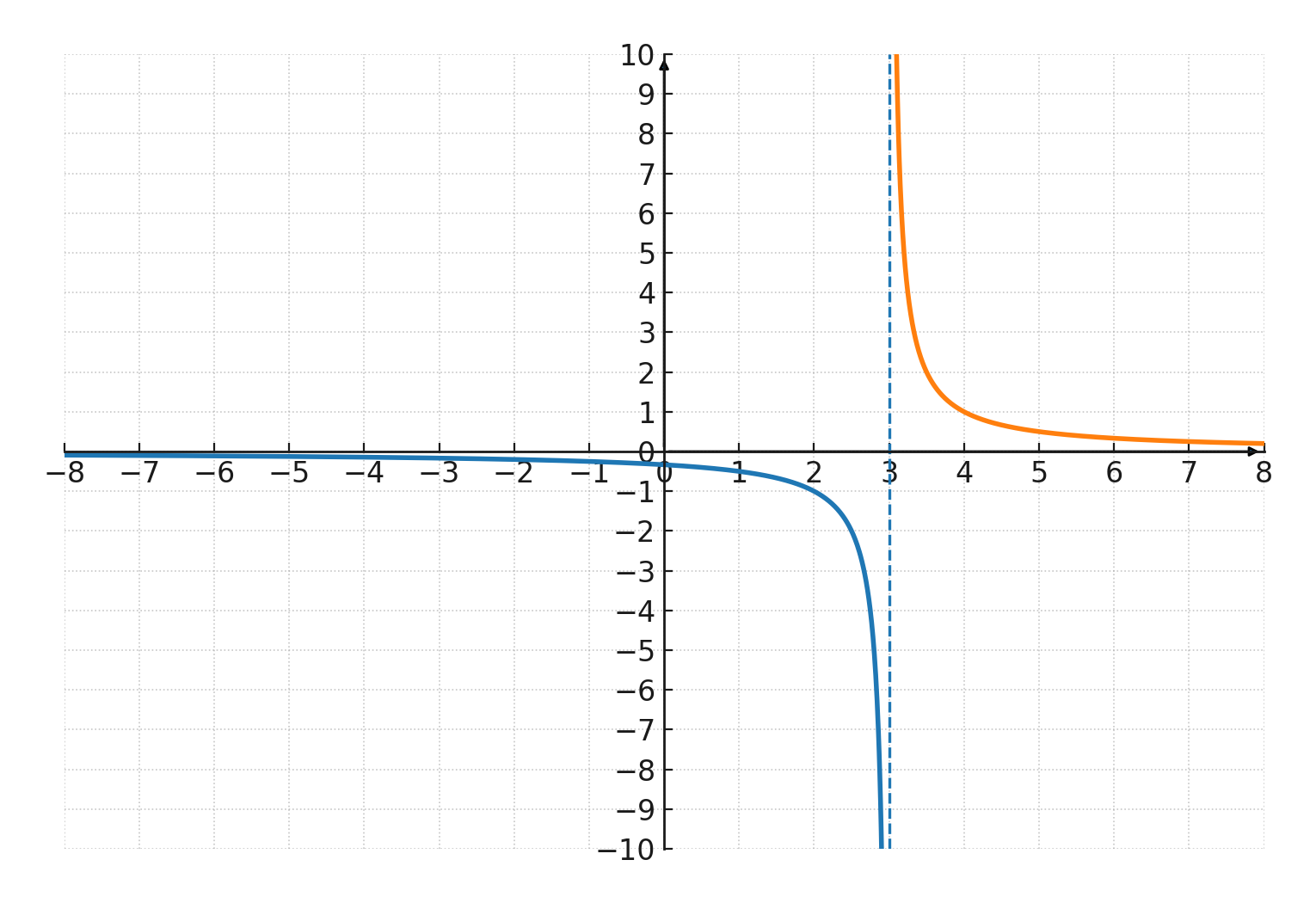
Aparecen cuando el denominador en una función racional se hace 0. Por ejemplo, la función \( \Large f(x) = \frac{1}{x-3} \) tiene una asíntota vertical en \(\large x = 3 \).

La función también tiene el eje x como una asíntota horizontal.

 

Asíntotas horizontales:

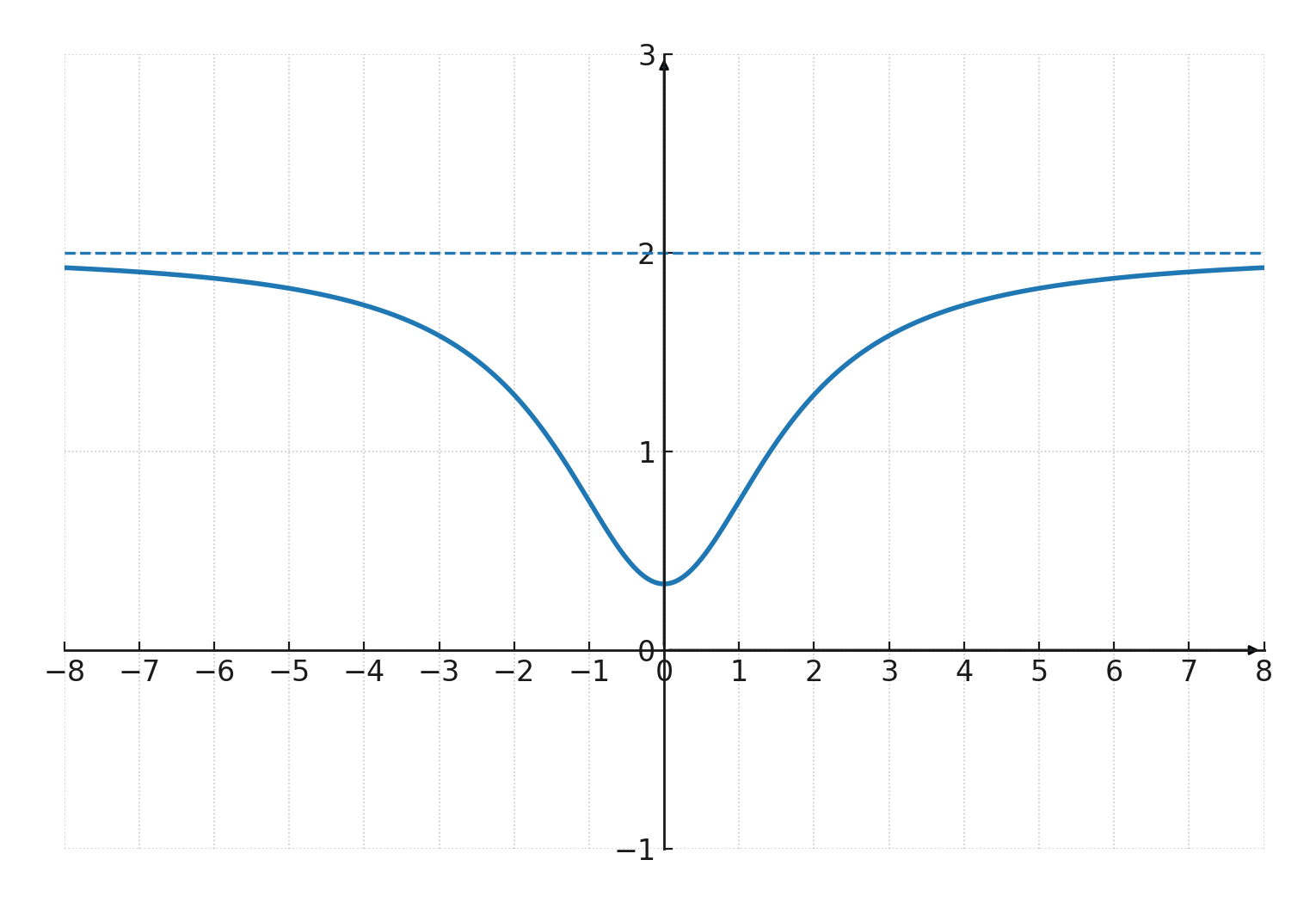
Aparecen cuando la gráfica de una función se aproxima a un valor constante al crecer o decrecer mucho \(\large x \).

Por ejemplo, \(\Large f(x) = \frac{2x^2+1}{x^2+3} \) tiene una asíntota horizontal en \(\large y = 2 \).

 

 

Asíntotas oblicuas:

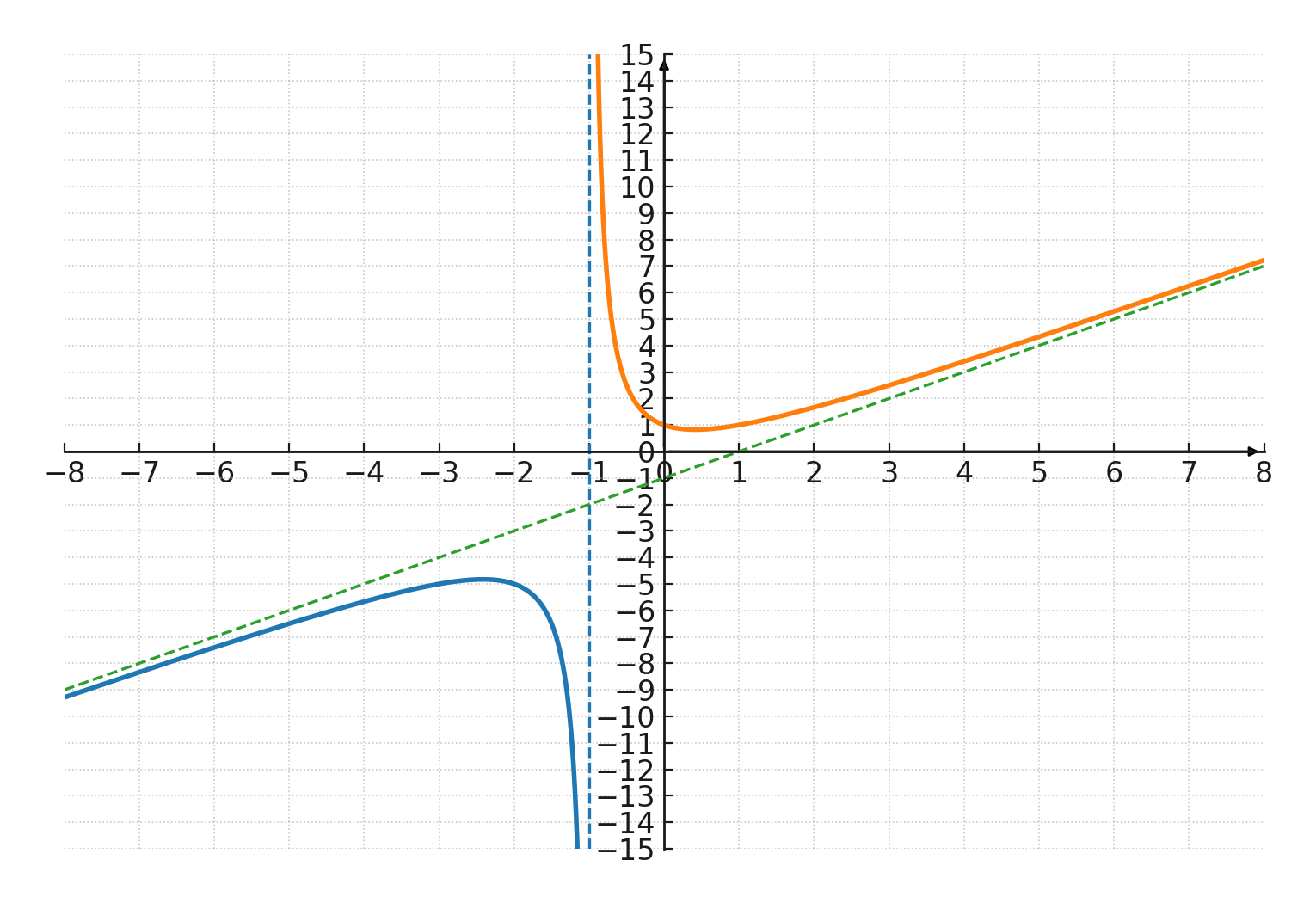
Aparecen cuando el grado del numerador es exactamente 1 mayor que el grado del denominador.

Por ejemplo, \(\Large f(x) = \frac{x^2+1}{x+1} \) tiene una asíntota oblicua en la recta \(\large y = x - 1 \).

 

 

Las asíntotas nos ayudan a comprender el comportamiento de una gráfica sin dibujarla completamente.