Función inversamente proporcional

Una función es inversamente proporcional cuando se cumple lo siguiente:

 

$$ y \cdot x=k $$

 

Es decir, si multiplicamos las dos coordenadas, x e y, el resultado siempre es la misma constante (k).

 

Por ejemplo, los siguientes pares de coordenadas:

 

$$ (1,20) = 1 \cdot 20 = 20 $$

$$ (2,10) = 2 \cdot 10 = 20 $$

$$ (4,5) = 4 \cdot 5 = 20 $$

$$ (5,4) = 5 \cdot 4 = 20 $$

$$ (10,2) = 10 \cdot 2 = 20 $$

$$ (20,1) = 20 \cdot 1 = 20 $$

 

Si representamos estos pares de coordenadas en un sistema, obtenemos la siguiente curva, que siempre tiene asíntotas a lo largo de ambos ejes.

Esto significa que puede acercarse mucho a los ejes, pero nunca los corta.

 

 

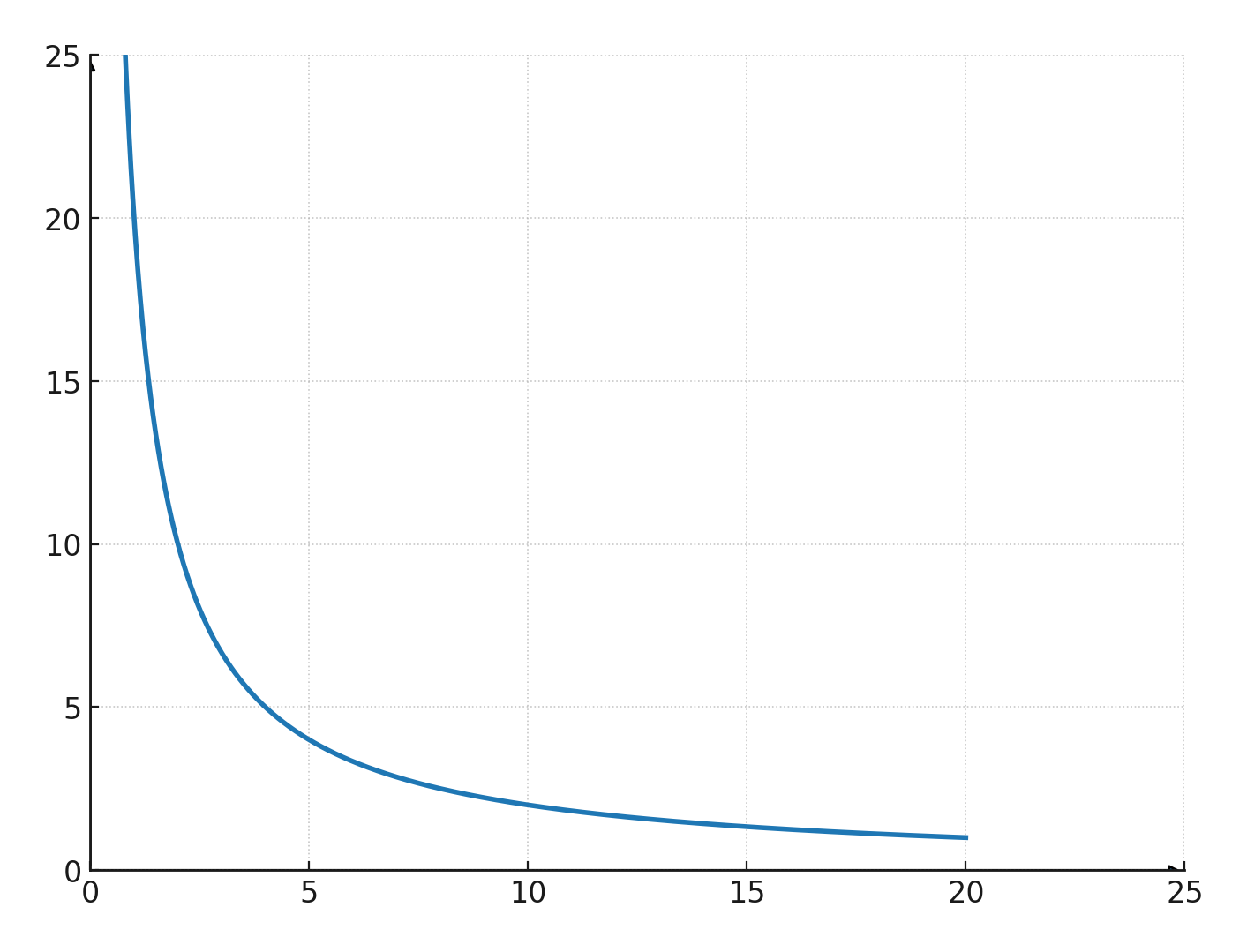
La constante k

k se llama la constante de proporcionalidad.

La expresión funcional de la proporcionalidad inversa se escribe así:

 

$$ f_{(x)} = \frac{k}{x} $$

 

\( x \) no puede ser 0. No se puede dividir por 0.

Si la constante es 15 y x = 5, entonces y = 3

 

$$ y = \frac{15}{5} $$

$$ y = 3 $$

 

De esta manera se pueden calcular más pares de coordenadas con la misma constante (15).

Observa que si has encontrado la coordenada \((5,3)\), también es válido \((3,5)\).

 

También puedes hacerlo con x = -5, entonces y = -3

 

$$ y = \frac{15}{-5} $$

$$ y = -3 $$

 

Si usas números negativos, podrás dibujar otra curva, que es un reflejo de la primera.

Estas curvas se llaman una Hipérbola.

 

Hipérbola

A continuación se muestra una hipérbola con la constante 15

Las coordenadas de la curva en el primer cuadrante se muestran en la tabla de valores:

 

\(\Large x \)	1	2	3	5	6	10	15
\(\Large y \)	15	7,5	5	3	2,5	1,5	1

 

 

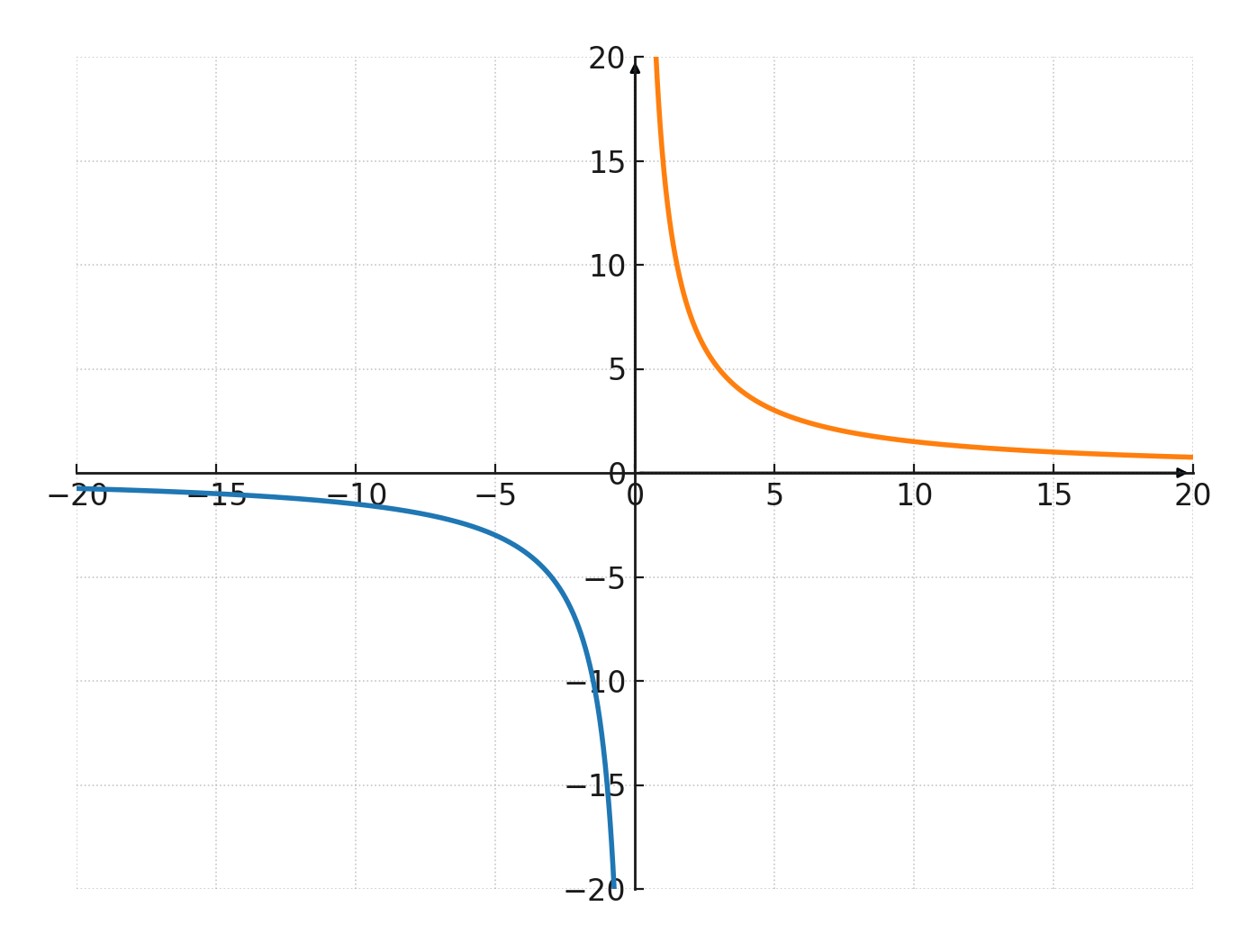
Para la curva en el tercer cuadrante también se cumple que \( x \cdot y = 15\)

 

\(\Large x \)	-1	-2	-3	-5	-6	-10	-15
\(\Large y \)	-15	-7,5	-5	-3	-2,5	-1,5	-1

 

En este ejemplo se han omitido algunas coordenadas por razones de espacio. Deberías calcular pares de coordenadas para todos los x de 1 a 15.

Así podrás dibujar una curva más precisa.