Función logarítmica

Una función logarítmica es la inversa de una función exponencial. Describe el número al que se debe elevar una base dada para obtener \(\large x\).

Se escribe de esta forma:

 

$$ \Large f(x)=\log_a(x) $$

 

Hay algunos requisitos para \(\large a\) y para \(\large x\):

 

• \(\large a>0\) y \(\large a \neq 1\)
  • La base no puede ser 1, de lo contrario el logaritmo no tiene variación
• \(\large x>0\)
  • El logaritmo solo está definido para valores positivos de \(\large x\)

 

Al dibujar una función logarítmica, se obtiene una curva que crece o decrece lentamente según la base.

• Si \(\large a>1\) la función es creciente
• Si \(\large 0

 

La gráfica tiene una asíntota vertical en \(\large x=0\). Corta el eje x en \(\large (1,0)\). No corta el eje y, ya que la función no está definida para \(\large x\le 0\).

 

Base y características

\(\large a\) se llama la base:

 

• La base determina si la gráfica es creciente o decreciente
• Cambiar la base estira o comprime la gráfica horizontalmente

 

El logaritmo también cumple la regla de cambio de base y las reglas de producto, pero aquí nos centramos en la forma de la gráfica.

 

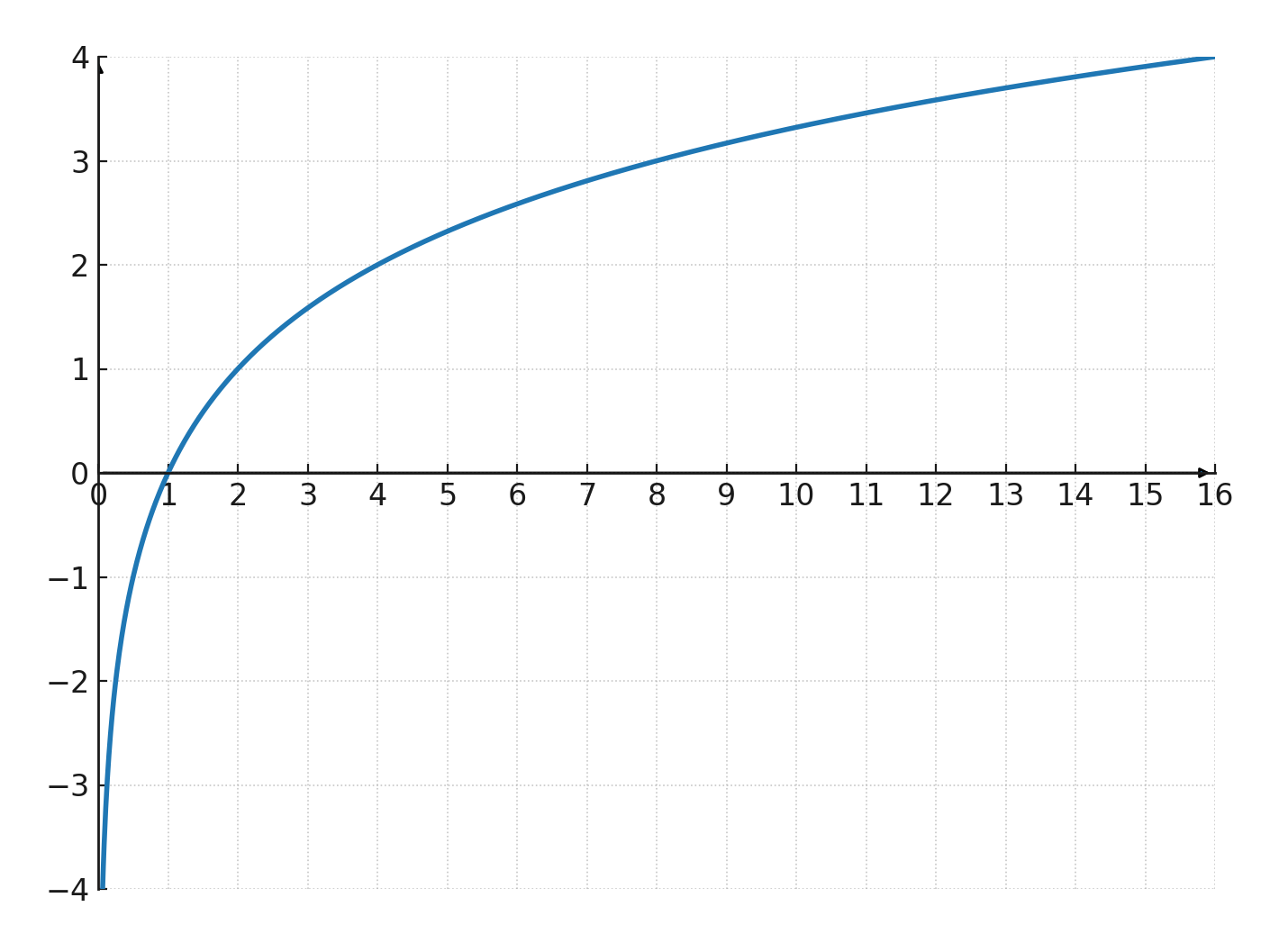
Si miramos esta función:

 

$$ \Large y=\log_2(x) $$

 

La curva es creciente, porque \(\large a=2\) es mayor que 1. Pasa por \(\large (1,0)\) y tiene una asíntota vertical en \(\large x=0\).

 

Ejemplo

Probamos la función \(\large y=\log_2(x)\)

 

\(\Large x\)	0.25	0.5	1	2	4
\(\Large y\)	-2	-1	0	1	2