Función de potencia

Una función de potencia es una función donde la variable $\large x$ aparece como base con un exponente fijo.

Se escribe de esta forma:

$$ \large f(x)=k \cdot x^a $$

Hay algunos requisitos para $\large k$ y $\large a$:

$\large k \neq 0$
- Si $\large k = 0$, la función siempre dará 0 en todos los casos, porque se multiplica por 0
$\large a$ puede ser un número entero, una fracción o un número negativo
- Si $\large a$ es un número entero positivo, se obtiene una curva polinómica creciente
- Si $\large a$ es una fracción, se obtiene una función radical
- Si $\large a$ es negativo, se obtiene una curva decreciente similar a una proporcionalidad inversa

Si se dibuja una función de potencia como gráfica, puede tener formas muy diferentes dependiendo del exponente $\large a$.

$\large a$ determina la forma y la simetría de la curva
$\large k$ determina cuán empinada es la curva y si se orienta hacia arriba o hacia abajo

La gráfica puede cortar el eje y en el origen, a menos que se añada una constante.

$\large a$ se llama el exponente:

Si $\large a$ es par, la curva se parecerá a una parábola y siempre estará en el mismo lado del eje x
Si $\large a$ es impar, la curva pasará por el origen y tendrá signos diferentes en las dos ramas

$\large k$ indica cuán rápidamente crece o decrece la curva

Si miramos esta función:

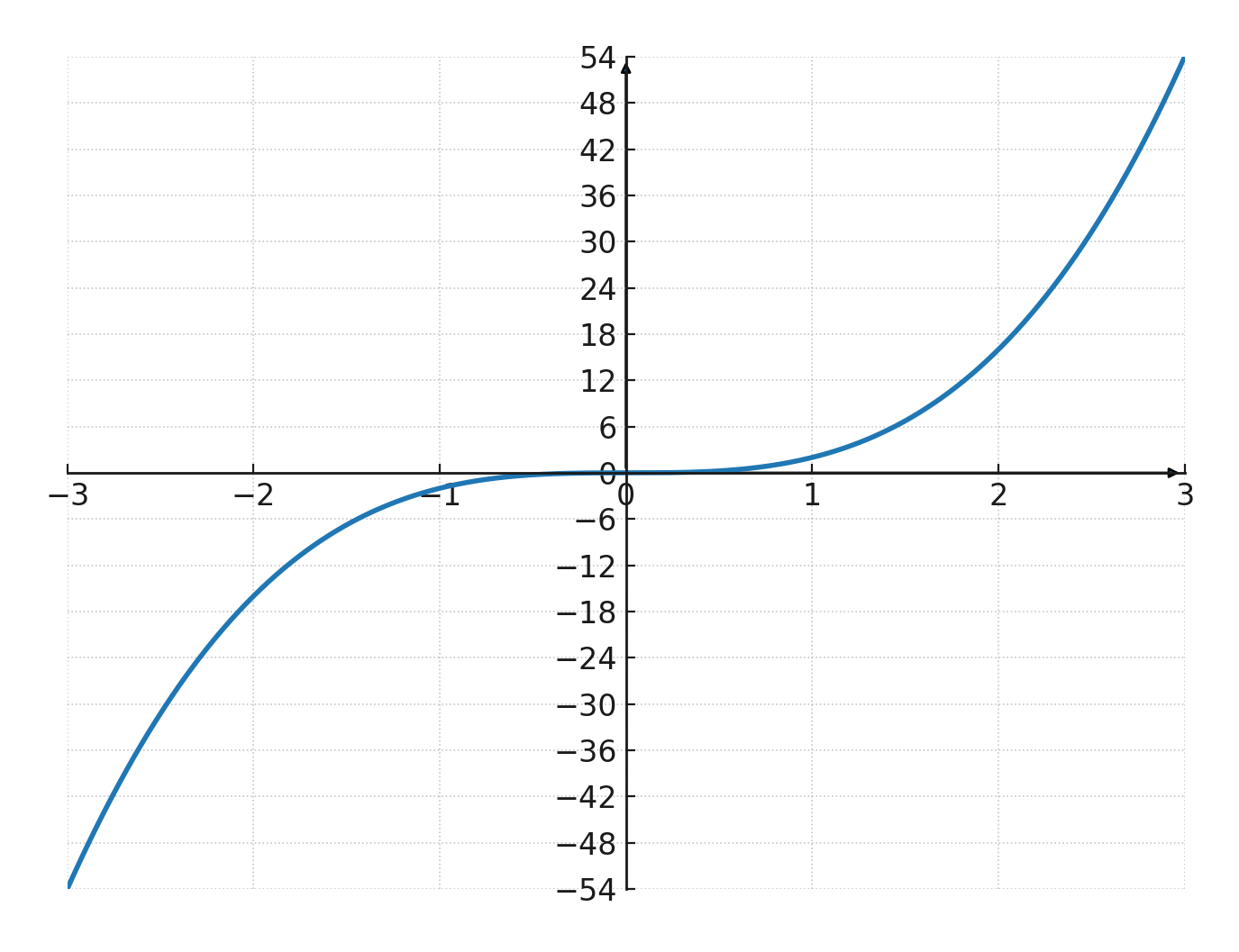
$$ \large y=2 \cdot x^3 $$

Podemos ver que es una función de potencia con $\large a=3$, lo que significa que la gráfica pasa por el origen y es impar.

También podemos ver que crece rápidamente, porque $\large k=2$ la hace más empinada que la función estándar $x^3$.

Probamos la función $\large y=2 \cdot x^3$

$\Large x$	-1	-2	-3	1	2	3
$\Large y$	-2	-16	-54	2	16	54

Función de potencia

\(\Large x\)	-1	-2	-3	1	2	3
\(\Large y\)	-2	-16	-54	2	16	54