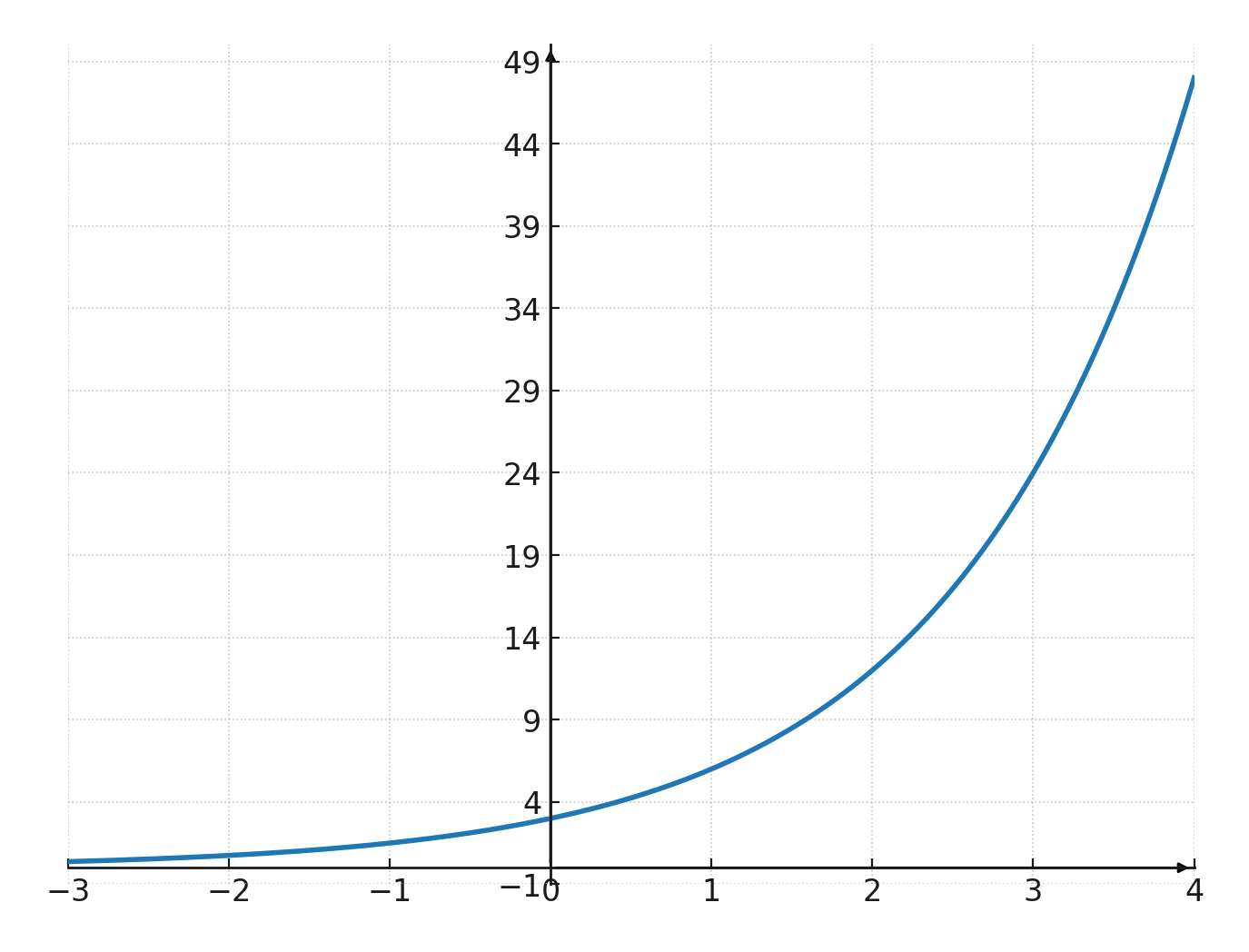
Función exponencial

Una función exponencial es una función donde la variable $\large x$ está en el exponente.

Se escribe de esta forma:

$$ \large f(x)=b \cdot a^x $$

Hay algunos requisitos para $\large a$ y $\large b$:

$\large a > 0$ y $\large a \neq 1$
- Si $\large a = 1 $, la función se convierte en constante sin ningún crecimiento
- Si $\large a \le 0$, la función no puede calcularse para todos los números reales, solo para números enteros
$\large b \neq 0$
- Si $\large b = 0 $, la función siempre dará 0 en todos los casos, porque se multiplica por 0

Si se dibuja una función exponencial como gráfico, será una curva pronunciada creciente o decreciente.

$\large a$ se llama factor de crecimiento y muestra qué tan rápido crece la curva
$\large b$ indica dónde la curva corta el eje y

La gráfica siempre estará en un lado del eje x.

El eje x funciona como una asíntota, lo que significa que la curva puede acercarse al eje pero nunca cortarlo.

$\large a$ se llama el factor de crecimiento:

$\large b$ indica que la curva cortará el eje y en $\large (0,b)$

Si miramos esta función:

$$ \large y=3 \cdot 2^x $$

Podemos ver que es una curva creciente, porque $\large a=2$

También podemos ver que corta el eje y en $(0,3)$

Probamos la función $\large y=3 \cdot 2^x$

$\large x$	1	2	3
$\large y$	6	12	24

Función exponencial

\(\large x\)	1	2	3
\(\large y\)	6	12	24