Quadratic function
Where a linear function is a first degree function, a quadratic function is a second degree function and is written in this form:
$$ \large f(x)=a \cdot x^2 + b \cdot x + c $$
\(\large a\) cannot be 0. If we insert 0 and multiply, it becomes nothing. The term disappears and what remains is a linear function
If you draw a quadratic function as a graph, it becomes a parabola, where the following applies:
- If \(\large a>0\) the arms point upwards
- If \(\large a<0\) the arms point downwards
- The parabola will always intersect the y-axis at \(\large (0,c) \)
- \(\large a \) determines how steep the parabola is, the larger \(\large a \), the narrower the parabola becomes
- The parabola is always symmetric about a vertical line through the vertex (the axis of symmetry)

Vertex and intersection
A quadratic function is related to quadratic equations.
To find the intersection with the x-axis, you must solve the quadratic equation where \( y=0\):
$$ \large 0=ax^2+bx+c $$
You must do as usual when solving quadratic equations.
The discriminant will tell you a little about the intersection of the parabola:
- If \( D > 0\) it intersects the x-axis in two places
- If \( D < 0\) it does not intersect the x-axis
- If \( D = 0\) it intersects the x-axis only once
To calculate the vertex of a parabola, we also use the discriminant:
$$ \large D= b^2-4ac $$
When we have the discriminant, we can calculate \((\large x,y)\) for the vertex:
$$ \large x=\frac{-b}{2a} $$
$$ \large y=\frac{-D}{4a} $$
Example intersection
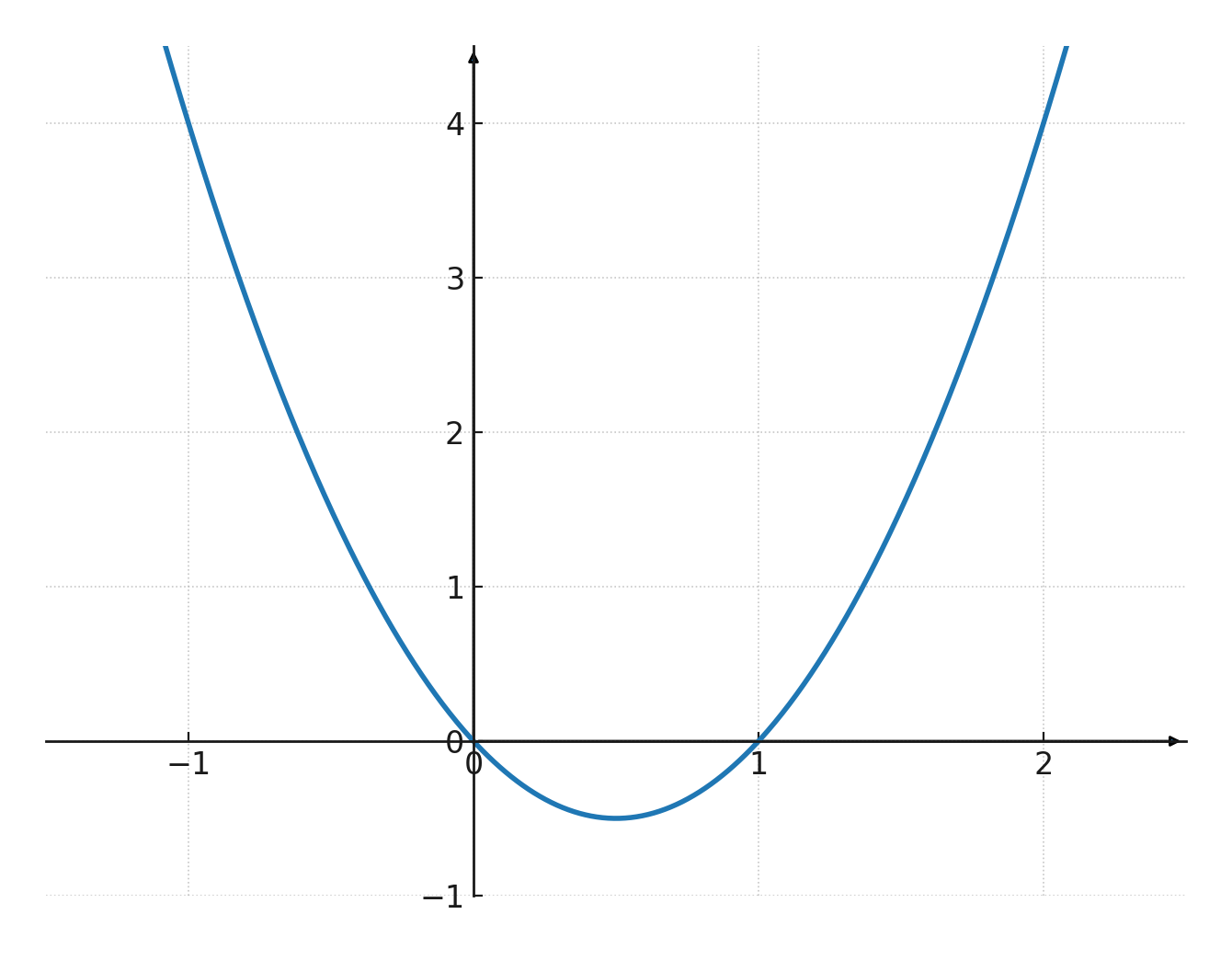
We try the function \(\large y=2x^2-2x+0\)
First, find the discriminant:
$$ D=b^2-4ac \Leftrightarrow $$
$$ D=2^2-4 \cdot 2 \cdot 0 \Leftrightarrow $$
$$ D=4 $$
The discriminant is positive.
This means that the parabola will intersect the x-axis in two places. We calculate the two places with the quadratic formula:
$$ \Large x= \frac{-b \pm \sqrt{d}}{2 \cdot a} $$
Intersection 1:
$$ \large x= \frac{-(-2) + \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2+2}{4} $$
$$ \large \underline{\underline{x= 1}} $$
Intersection 2:
$$ \large x= \frac{-(-2) - \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2-2}{4} $$
$$ \large \underline{\underline{x= 0}} $$
Example vertex
In the example we found that the discriminant is 4
Now we can calculate \((x,y)\) for the vertex:
$$ \large x=\frac{-b}{2a} \Leftrightarrow $$
$$ \large x=\frac{-(-2)}{2\cdot 2} \Leftrightarrow $$
$$ \large x=0.5 $$
$$ \large y=\frac{-D}{4a} \Leftrightarrow $$
$$ \large y=\frac{-4}{4 \cdot 2} \Leftrightarrow $$
$$ \large y=-0.5 $$
Vertex = \((0.5, -0.5)\)
Coordinate sets
We now have three coordinate sets, the two intersections and the vertex:
$$ \large (0,0), (0.5, -0.5), (0,1) $$
We could draw the parabola with these three, but let’s find two more, by inserting -1 and 2 into the function:
$$ \large y=2 \cdot -1^2-2 \cdot -1+0 $$
$$ \large y=4 $$
$$ \large y=2 \cdot 2^2-2 \cdot 2+0 $$
$$ \large y=4 $$
| \(x\) | 0 | 0,5 | 0 | -1 | 2 |
| \(y\) | 0 | -0,5 | 1 | 4 | 4 |
Now it can be drawn.