Cubic function

A cubic function is a third-degree function. The general formula looks like this:

 

$$ \large f(x) = a \cdot x^3 + b \cdot x^2 + c \cdot x + d $$

 

Here \( \large a \neq 0\), otherwise multiplication by 0 would make the function a quadratic function.

 

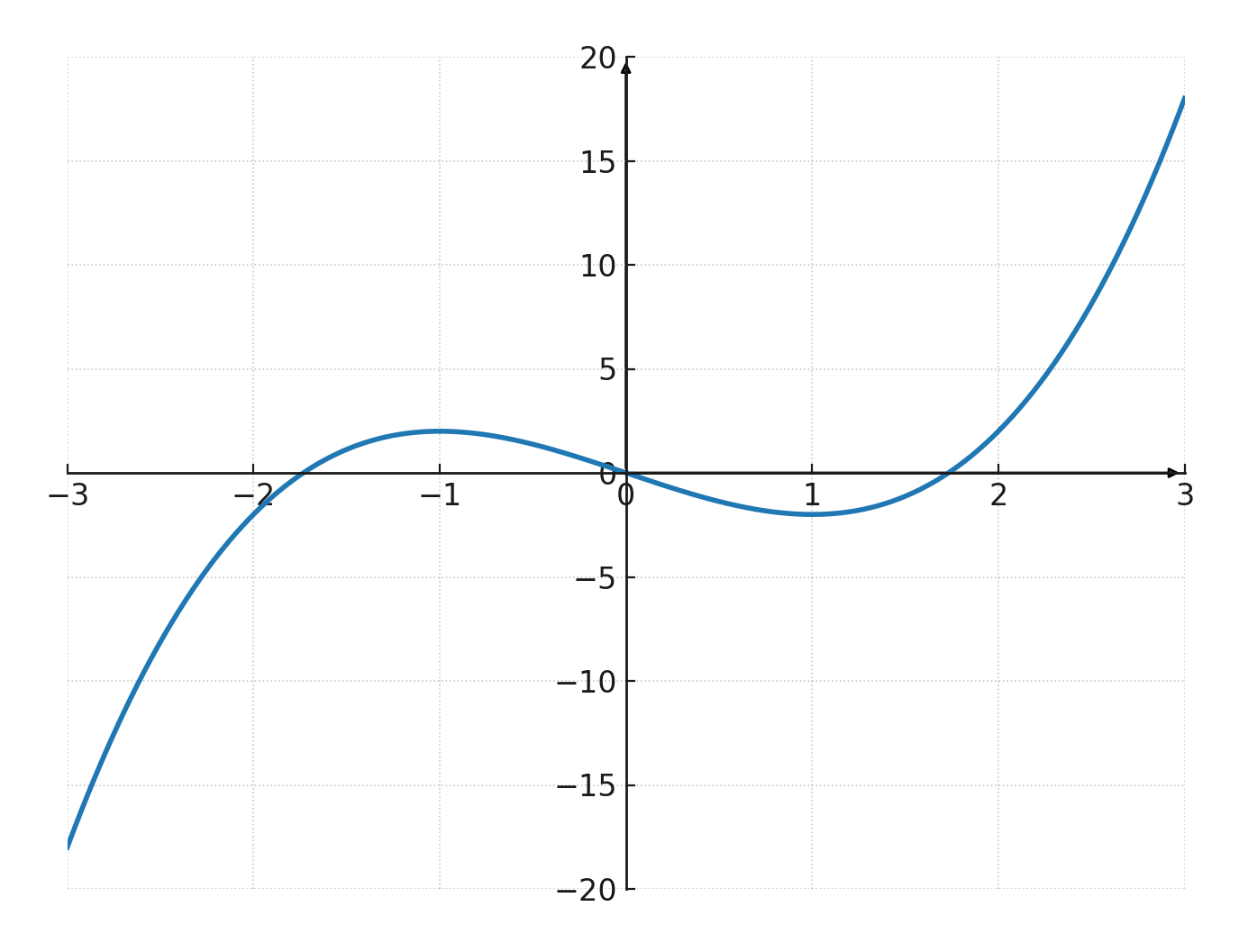
The graph of a cubic function is called a cubic curve. It typically has an S-shape, but can vary depending on the coefficients.

 

• If \( \large a > 0\), the graph starts in the lower left corner and ends in the upper right corner.
• If \( \large a < 0\), the graph starts in the upper left corner and ends in the lower right corner.

 

 

Roots

A cubic function can have one or three intersections with the x-axis, depending on the discriminant.

A root is the point where it either intersects or touches the x-axis, i.e. where \( \large f(x) = 0 \). Therefore, it always has at least one real root and up to three real roots.

 

Local maxima and minima

A cubic function can have both a local maximum (peak) and a local minimum (valley) if the discriminant allows it. In that case the graph takes its characteristic S-shape.

If the conditions are not met, the graph will simply rise or fall without bending.

 

Other important points

• The graph intersects the y-axis at \( \large (0,d)\)
• The graph always has an inflection point at \( \large x=-\frac{b}{3a}\)
• The expression \( \large b^2 - 3ac \) determines the shape of the graph
  • If \( \large b^2-3ac>0\), there are two extrema (one maximum and one minimum).
  • If \( \large b^2-3ac=0\), there is one double stationary point.
  • If \( \large b^2-3ac<0\), there are no extrema.

 

Example

Let us try this function:

 

$$ \large f(x) = x^3 - 3x + 2 $$

 

Here \( \large a = 1\), \( \large b = 0\), \( \large c = -3\), \( \large d = 2\).

 

The function gives the following coordinate set:

\( x \)	-2	-1	0	1	2	3
\( y \)	-4	4	2	0	4	20

 

 

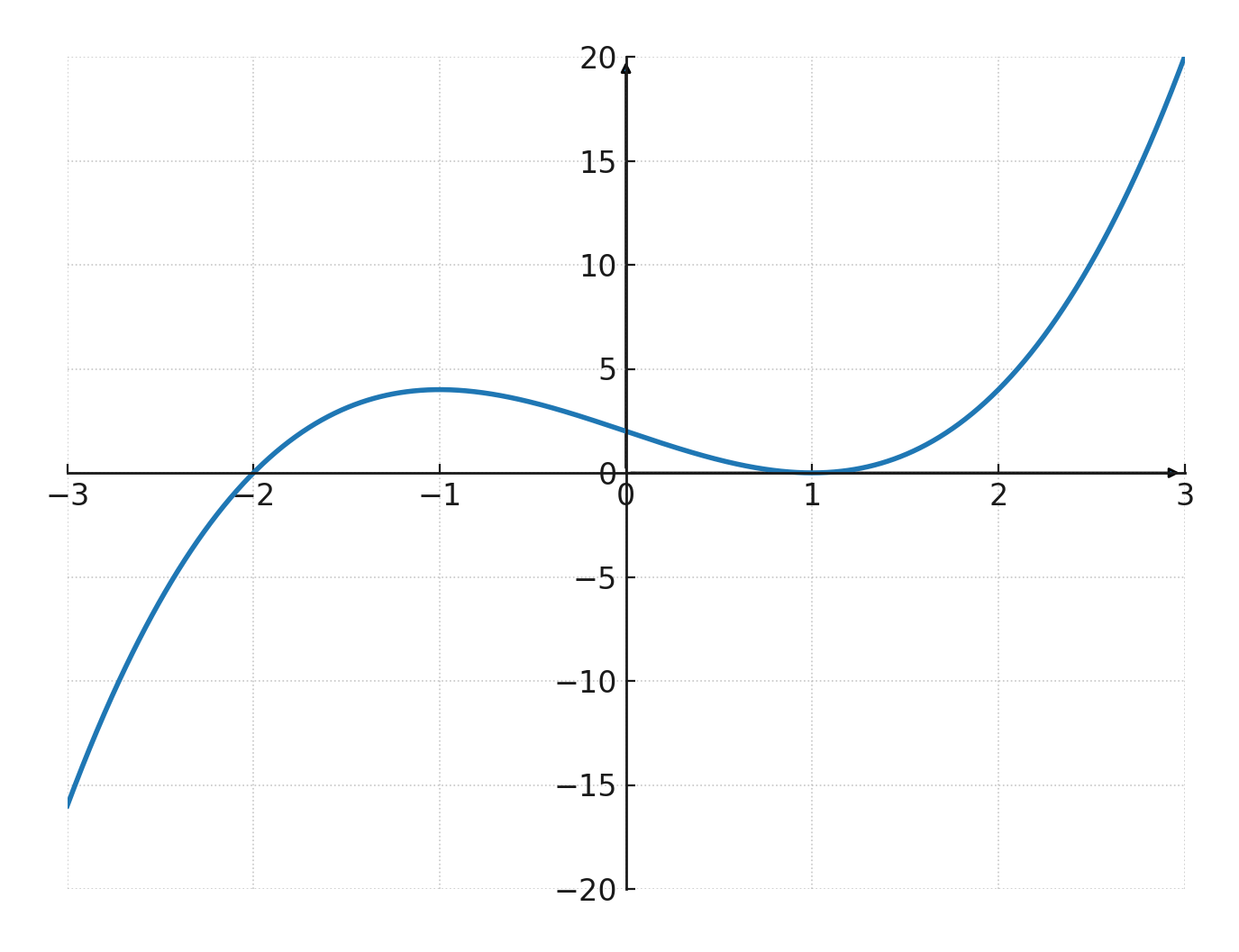
It is possible to factorize the function:

$$ \large f(x) = (x+2)(x-1)^2 $$

 

Thus the graph has the roots \( \large (-2,0)\) and \( \large (1,0)\). The point \( \large (1,0)\) is a double root, which means the graph touches the x-axis here without crossing it.

If instead it had crossed through this point, the function would have had three distinct roots.

 

The graph intersects the y-axis at \( \large (0,2)\).

 

The discriminant gives \( \large b^2 - 3ac = 0^2 - 3 \cdot 1 \cdot (-3) = 9 > 0\), so the function has both a local maximum and a local minimum. Therefore the graph takes the classical S-shape.