Polynomials
A polynomial is a specific type of mathematical function, built from terms where a variable (typically called x) is raised to different powers and multiplied by numbers (coefficients). Finally, several of these terms can be added together.
The simplest type of polynomial is a constant function. It is called a 0th degree polynomial, because no x is included. The function always has the same value, no matter what x is.
An example is:
$$ \large f(x) = 5 $$
Here the value is always 5, whether x is -10, 0 or 100. The graph is therefore a horizontal line parallel to the x-axis.
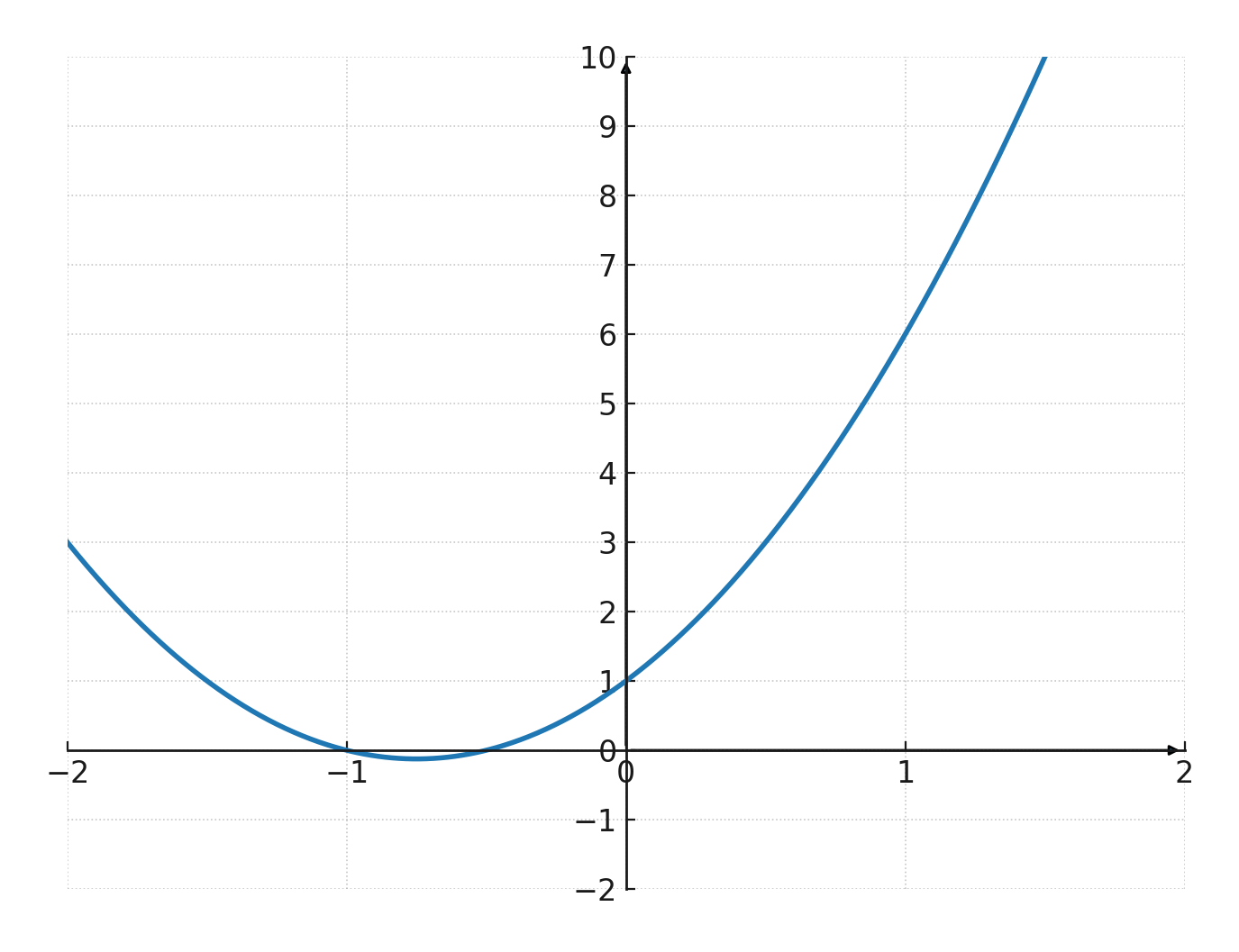
Here is an example of a 2nd degree polynomial. It is also called a quadratic function:
$$ \large f(x) = 2x^2 + 3x + 1 $$
Here there are three terms: \(2x^2\), \(3x\) and \(1\). If you draw it as a graph, it will be a parabola:
The degree of a polynomial
The highest power of x (the exponent) is called the degree of the polynomial:
- 0th degree: Constant function, e.g. \( f(x)=5 \).
- 1st degree: Linear function, e.g. \( f(x)=2x+1 \).
- 2nd degree: Quadratic function, e.g. \( f(x)=x^2-3x+2 \).
- 3rd degree: Cubic function, e.g. \( f(x)=x^3-3x+2 \).
From 4th degree and higher, one usually just uses the term n-th degree polynomial instead of a special name.
The higher the degree, the more complex the graphs become, and the curves can bend in more ways.
An infinite family
Polynomials form an entire family of functions.
There are polynomials of all degrees, and therefore one can say that it is in principle an infinite sequence of functions. Each polynomial has its own specific graph, depending on the degree and the numbers used as coefficients.
Where are polynomials used?
Polynomials are important because they appear in many areas of mathematics and in real life:
- In economics, a function can describe the development of interest or investment.
- In physics, a function can describe motion or velocity.
- In statistics, they help fit curves to data.
Even though polynomials sound technical, they are fundamental building blocks of mathematics, giving us tools to describe and understand everything from a simple straight line to much more complicated relationships.