Linear function

A linear function is written in this form:

$$ \large f(x)=a \cdot x + b $$

If a linear function is drawn as a graph, it will always be a straight line.

The graph can be increasing, decreasing or horizontal depending on $ \large a$, and $ \large b$ tells us where it cuts the y axis

$ \large a$ is called the slope:

If $ \large a > 0$ the line is increasing from left to right
If $ \large a < 0$ the line is decreasing from left to right
If $ \large a = 0$ the line is horizontal, because no matter what $\large x$ is, $\large y$ is always the same.

$ \large b$ tells that the line will cut the y axis at the point $(0,b)$

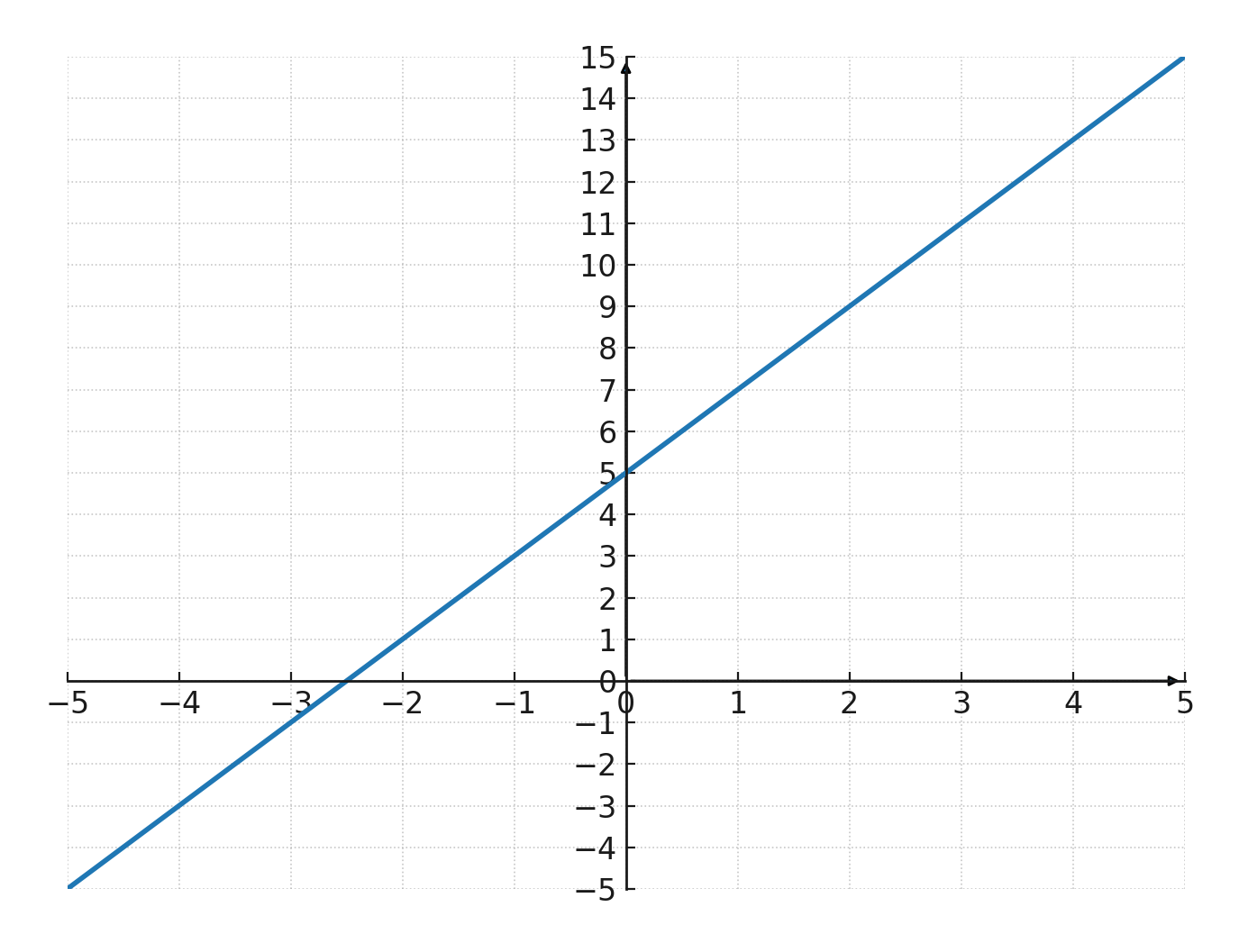
If we look at this function:

$$ \large y=2x+5 $$

Then we can see that it is an increasing line, because $\large a=2$.

We can also see that it will cut the y axis at $(0,5)$, because $\large b=5$.

We try the function: $ \large y=2x+5 $

The coordinates are entered in the value table below and then in the coordinate system, so the graph can be drawn:

$\large x$	1	2	3	4	5
$\large y$	7	9	11	13	15

Linear function

If we have the coordinates $(2,9)$ and $(4,13)$, it is possible to find $\large a$ and $\large b$ in the following way:

$$ \large a = \frac{y_2-y_1}{x_2-x_1} \Leftrightarrow $$

$$ \large a = \frac{13-9}{4-2} \Leftrightarrow $$

$$ \large a = \frac{4}{2} \Leftrightarrow $$

$$ \large a = 2 $$

When we have found $\large a$, we can also find $\large b$, with one of these two formulas. (It does not matter which one you use)

$$ \large b = y_1 - a \cdot x_1 $$

$$ \large b = y_2 - a \cdot x_2 $$

We use the first one:

$$ \large b = 9 - 2 \cdot 2 \Leftrightarrow $$

$$ \large b = 9 - 4 \Leftrightarrow $$

$$ \large b = 5 $$

The function rule for the coordinates $(2,9)$ and $(4,13)$ is therefore

$$ \large y = ax + b $$

$$ \large y = 2x + 5 $$

\(\large x\)	1	2	3	4	5
\(\large y\)	7	9	11	13	15