Eksponentiel funktion

En eksponentiel funktion er en funktion hvor variablen $\large x$ står i eksponenten.

Den skrives på denne form:

$$ \large f(x)=b \cdot a^x $$

Der er nogle krav til $\large a$ og $\large b$:

$\large a > 0$ og $\large a \neq 1$
- Hvis $\large a = 1 $, bliver funktionen konstant uden nogen udvikling
- Hvis $\large a \le 0$, vil funktionen ikke kunne regnes for alle reelle tal, men kun for heltal
$\large b \neq 0$
- Hvis $\large b = 0 $, vil funktionen i alle tilfælde altid give 0, fordi der ganges med 0

Hvis man tegner en eksponentiel funktion som graf, vil den blive til en stejl stigende eller faldende kurve.

$\large a$ kaldes for fremskrivningsfaktoren og fortæller hvor hurtigt væksten i kurven stiger
$\large b$ fortæller hvor kurven skærer y-aksen

Grafen vil altid ligge på den ene side af x-aksen.

X-aksen fungerer som en asymptote, hvilket betyder, at kurven kan nærme sig aksen, men den kan aldrig skære den.

$\large a$ kaldes for fremskrivningsfaktoren:

$\large b$ fortæller at kurven vil skære y-aksen i $\large (0,b)$

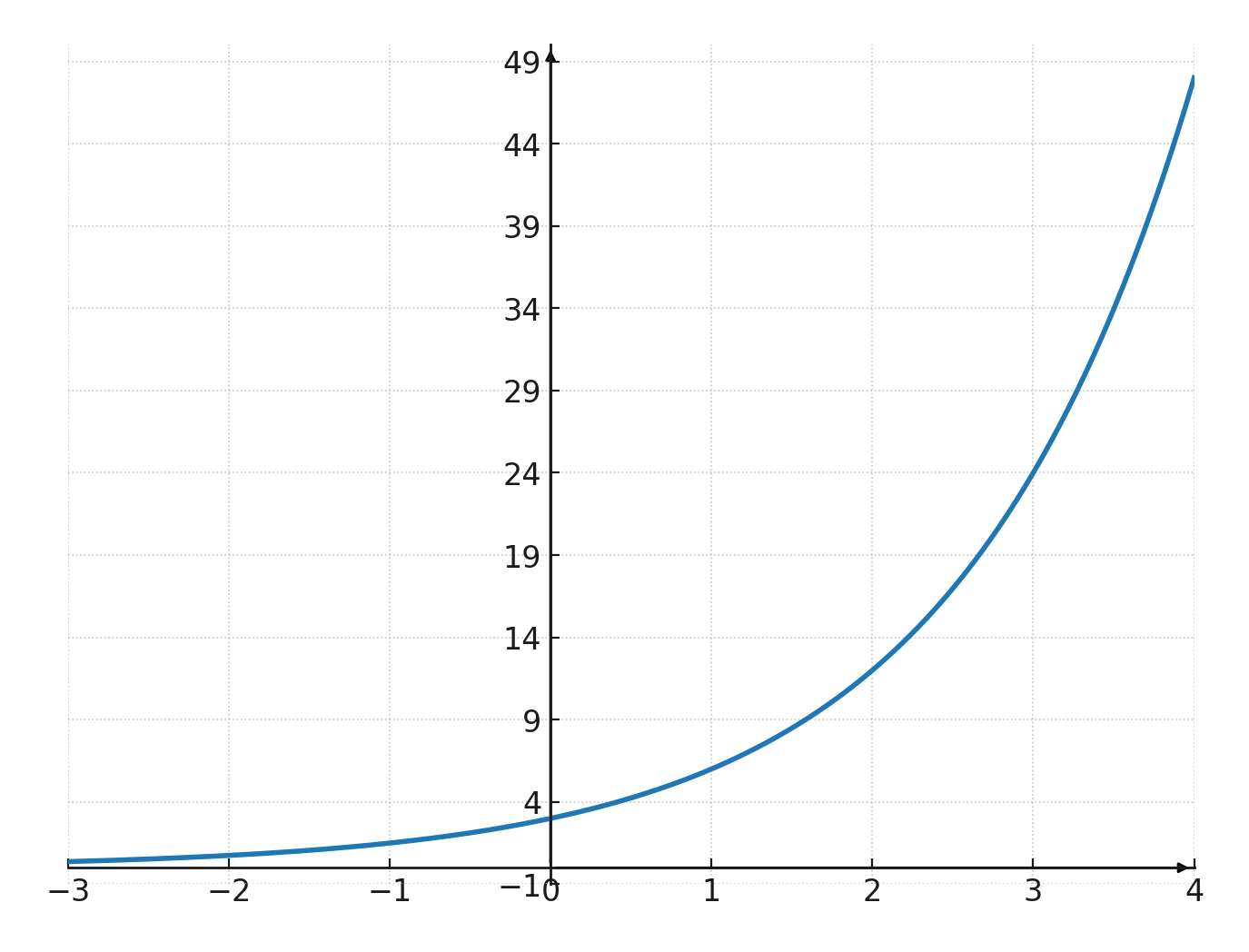
Hvis vi ser på denne funktion:

$$ \large y=3 \cdot 2^x $$

Så kan vi se at det er en stigende kurve, fordi $\large a=2$

Vi kan også se, at den skærer y-aksen i $(0,3)$

Vi prøver funktionen $\large y=3 \cdot 2^x$

$\Large x$	1	2	3
$\Large y$	6	12	24

Eskponentiel funktion

\(\Large x\)	1	2	3
\(\Large y\)	6	12	24