Brøkfunktioner

En brøkfunktion er et synonym for en rationel funktion.

Det vil sige en funktion skrevet som:

$ \large f(x) = \frac{P(x)}{Q(x)} $

Når man analyserer en brøkfunktion, går man typisk frem i denne rækkefølge:

Først finder man domænet, derefter nulpunkter, så skæring med y-aksen og til sidst asymptoter.

Det giver en sammenhængende beskrivelse af grafen.

Domæne:

Domænet er mængden af alle tilladte x-værdier for funktionen.

For en brøkfunktion er domænet alle reelle x, hvor $\large Q(x)\neq 0 $.

Hvis både tæller og nævner bliver 0 i samme x (fælles faktor), er punktet stadig udelukket fra domænet og ses som et hul i grafen.

Hvis $\large Q(x)=0 $ men $\large P(x)\neq 0 $, får man typisk en lodret asymptote.

Nulpunkter:

Grafen har nulpunkter i de punkter, hvor tælleren er 0, forudsat at nævneren ikke også er 0 i samme punkt.

Skæring med y-aksen:

Findes ved at indsætte $ \large x = 0 $, hvis dette ligger inden for domænet.

Asymptoter:

Lodrette asymptoter optræder typisk ved de $ \large x $-værdier, hvor nævneren er 0. Vandrette eller skrå asymptoter findes ved at sammenligne graderne af tæller og nævner eller ved polynomiumdivision.

Et eksempel er funktionen:

$$ \large f(x) = \frac{x^2 - 1}{x^2 - 4} $$

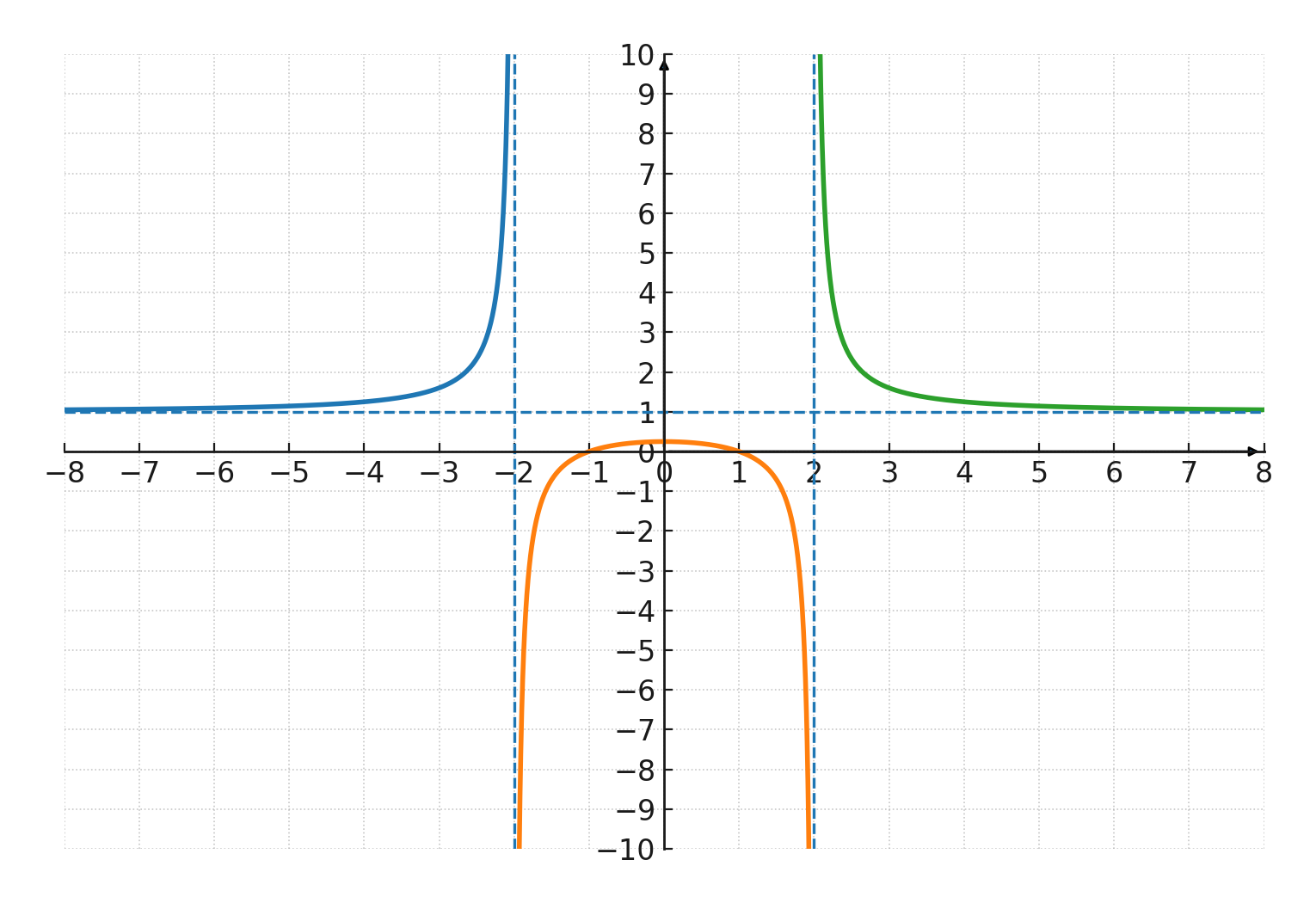
Rational funktion med flere lodrette asymptoter

Her er tælleren $ \large x^2 - 1 $, som giver nulpunkter ved $ \large x = 1 $ og $ \large x = -1 $.

Nævneren $ \large x^2 - 4 $ bliver 0 ved $ \large x = -2 $ og $ \large x = 2 $, så funktionen er ikke defineret der.

Domænet er altså alle reelle $ \large x $ bortset fra $ \large -2 $ og $ \large 2 $. Grafen har lodrette asymptoter ved $ \large x = -2 $ og $ \large x = 2 $.

Da graden i tæller og nævner er ens, fås en vandret asymptote ved $ \large y = 1 $. Skæringen med y-aksen findes ved $ \large x = 0 $: $ \large f(0) = \frac{-1}{-4} = \frac{1}{4} $

Med denne fremgangsmåde får man et samlet overblik over brøkfunktioners opførsel.