Logaritme funktion

En logaritmefunktion er den omvendte til en eksponentiel funktion. Den beskriver det tal, som en given base skal opløftes i for at give \(\large x\).

Den skrives på denne form:

 

$$ \Large f(x)=\log_a(x) $$

 

Der er nogle krav til \(\large a\) og til \(\large x\):

 

• \(\large a>0\) og \(\large a \neq 1\)
  • Basen må ikke være 1, for så giver logaritmen ingen variation
• \(\large x>0\)
  • Logaritmen er kun defineret for positive \(\large x\)-værdier

 

Når man tegner en logaritmefunktion, får man en kurve der enten stiger eller falder langsomt afhængigt af basen.

• Hvis \(\large a>1\) er funktionen voksende
• Hvis \(\large 0<a<1\) er funktionen aftagende

 

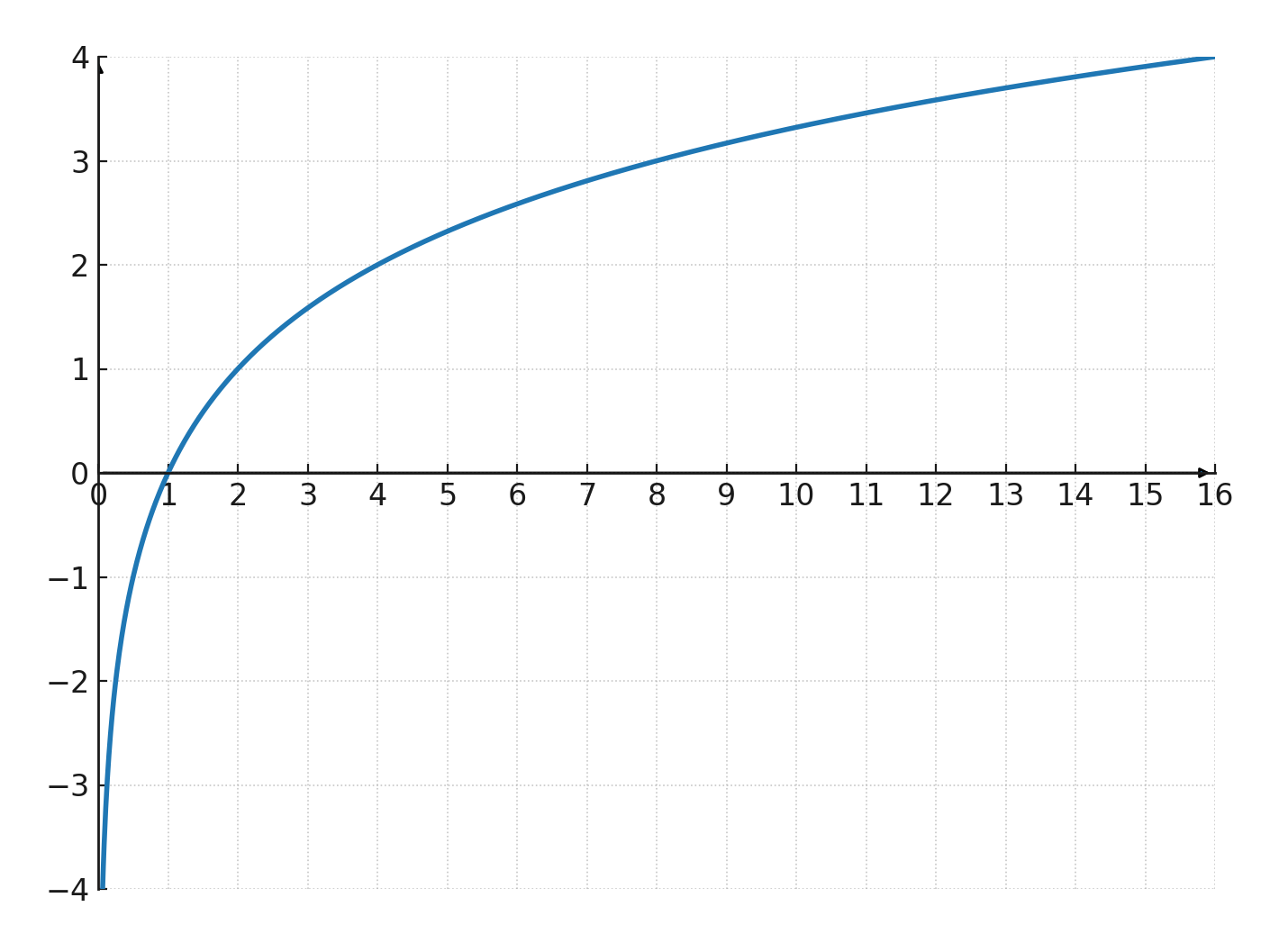
Grafen har en lodret asymptote langs \(\large x=0\). Den skærer x-aksen i \(\large (1,0)\). Den skærer ikke y-aksen, da funktionen ikke er defineret for \(\large x\le 0\).

 

Base og karakteristika

\(\large a\) kaldes for basen:

 

• Basen bestemmer om grafen er voksende eller aftagende
• Ændring af basen strækker eller komprimerer grafen vandret

 

Logaritmen opfylder også basebytning og produkt-regler, men her fokuserer vi på selve grafens form.

 

Hvis vi ser på denne funktion:

 

$$ \Large y=\log_2(x) $$

 

Så er kurven voksende, fordi \(\large a=2\) er større end 1. Den går gennem \(\large (1,0)\) og har en lodret asymptote ved \(\large x=0\).

 

Eksempel

Vi prøver funktionen \(\large y=\log_2(x)\)

 

\(\Large x\)	0.25	0.5	1	2	4
\(\Large y\)	-2	-1	0	1	2