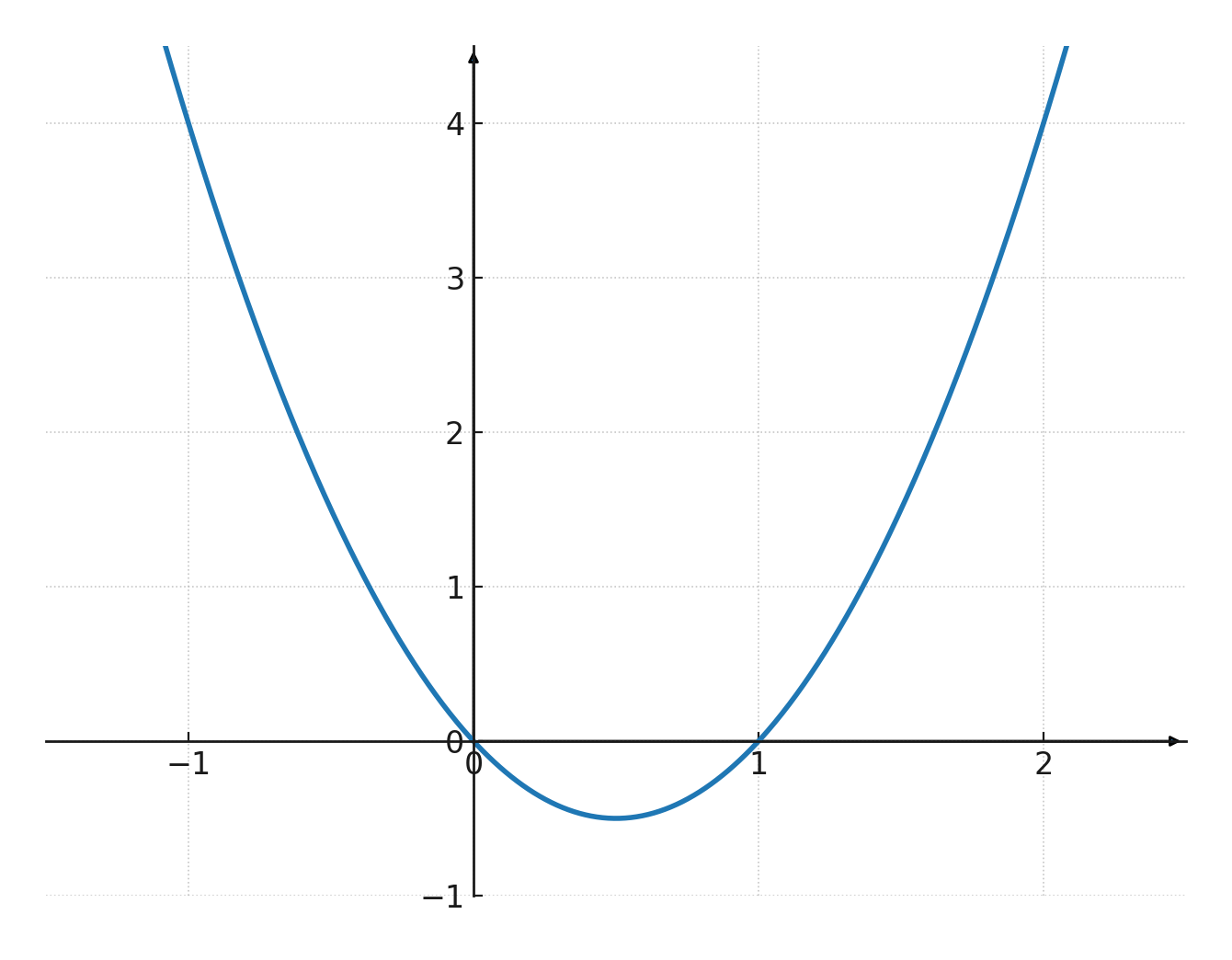
Quadratische Funktion
Wo eine lineare Funktion eine Funktion ersten Grades ist, ist eine quadratische Funktion eine Funktion zweiten Grades und wird in dieser Form geschrieben:
$$ \large f(x)=a \cdot x^2 + b \cdot x + c $$
\(\large a\) darf nicht 0 sein. Wenn wir 0 einsetzen und multiplizieren, bleibt nichts übrig. Das Glied verschwindet und es bleibt eine lineare Funktion
Wenn du eine quadratische Funktion als Graph zeichnest, wird sie zu einer Parabel, bei der Folgendes gilt:
- Wenn \(\large a>0\) zeigen die Arme nach oben
- Wenn \(\large a<0\) zeigen die Arme nach unten
- Die Parabel schneidet immer die y-Achse bei \(\large (0,c) \)
- \(\large a \) bestimmt, wie steil die Parabel ist, je größer \(\large a \), desto schmaler wird sie
- Die Parabel ist immer symmetrisch zu einer senkrechten Linie durch den Scheitelpunkt (die Symmetrieachse)
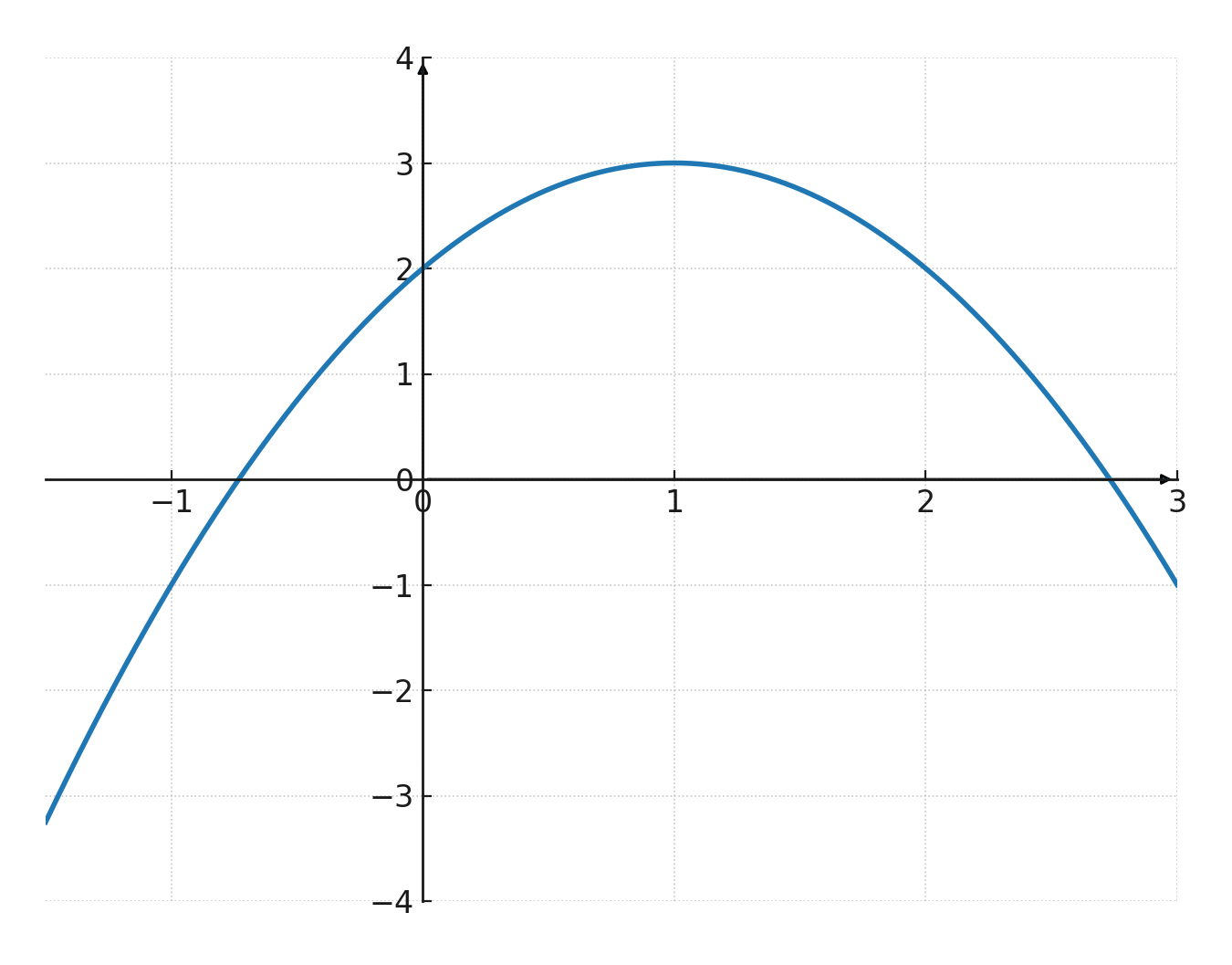
Scheitelpunkt und Schnittpunkt
Eine quadratische Funktion hängt mit quadratischen Gleichungen zusammen.
Um den Schnittpunkt mit der x-Achse zu finden, musst du die quadratische Gleichung lösen, bei der \( y=0\):
$$ \large 0=ax^2+bx+c $$
Du musst wie gewohnt vorgehen, wenn du quadratische Gleichungen berechnest.
Die Diskriminante sagt dir etwas über den Schnittpunkt der Parabel:
- Wenn \( D > 0\) schneidet sie die x-Achse an zwei Stellen
- Wenn \( D < 0\) schneidet sie die x-Achse nicht
- Wenn \( D = 0\) schneidet sie die x-Achse nur einmal
Um den Scheitelpunkt einer Parabel zu berechnen, verwenden wir auch die Diskriminante:
$$ \large D= b^2-4ac $$
Wenn wir die Diskriminante haben, können wir \((\large x,y)\) für den Scheitelpunkt berechnen:
$$ \large x=\frac{-b}{2a} $$
$$ \large y=\frac{-D}{4a} $$
Beispiel Schnittpunkt
Wir probieren die Funktion \(\large y=2x^2-2x+0\)
Zuerst finden wir die Diskriminante:
$$ D=b^2-4ac \Leftrightarrow $$
$$ D=2^2-4 \cdot 2 \cdot 0 \Leftrightarrow $$
$$ D=4 $$
Die Diskriminante ist positiv.
Das bedeutet, dass die Parabel die x-Achse an zwei Stellen schneidet. Wir berechnen die beiden Stellen mit der Mitternachtsformel:
$$ \Large x= \frac{-b \pm \sqrt{d}}{2 \cdot a} $$
Schnittpunkt 1:
$$ \large x= \frac{-(-2) + \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2+2}{4} $$
$$ \large \underline{\underline{x= 1}} $$
Schnittpunkt 2:
$$ \large x= \frac{-(-2) - \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2-2}{4} $$
$$ \large \underline{\underline{x= 0}} $$
Beispiel Scheitelpunkt
Im Beispiel haben wir herausgefunden, dass die Diskriminante 4 ist
Nun können wir \((x,y)\) für den Scheitelpunkt berechnen:
$$ \large x=\frac{-b}{2a} \Leftrightarrow $$
$$ \large x=\frac{-(-2)}{2\cdot 2} \Leftrightarrow $$
$$ \large x=0,5 $$
$$ \large y=\frac{-D}{4a} \Leftrightarrow $$
$$ \large y=\frac{-4}{4 \cdot 2} \Leftrightarrow $$
$$ \large y=-0,5 $$
Scheitelpunkt = \((0,5, -0,5)\)
Koordinatensätze
Wir haben nun drei Koordinatensätze, die beiden Schnittpunkte und den Scheitelpunkt:
$$ \large (0,0), (0,5, -0,5), (0,1) $$
Man könnte die Parabel mit diesen drei Punkten zeichnen, aber wir finden noch zwei weitere, indem wir -1 und 2 in die Funktion einsetzen:
$$ \large y=2 \cdot -1^2-2 \cdot -1+0 $$
$$ \large y=4 $$
$$ \large y=2 \cdot 2^2-2 \cdot 2+0 $$
$$ \large y=4 $$
| \(x\) | 0 | 0,5 | 0 | -1 | 2 |
| \(y\) | 0 | -0,5 | 1 | 4 | 4 |
Nun kann sie gezeichnet werden.