Exponentialfunktion

Eine Exponentialfunktion ist eine Funktion, bei der die Variable $\large x$ im Exponenten steht.

Sie wird in dieser Form geschrieben:

$$ \large f(x)=b \cdot a^x $$

Es gibt einige Bedingungen für $\large a$ und $\large b$:

$\large a > 0$ und $\large a \neq 1$
- Wenn $\large a = 1 $, wird die Funktion konstant ohne Entwicklung
- Wenn $\large a \le 0$, kann die Funktion nicht für alle reellen Zahlen berechnet werden, sondern nur für ganze Zahlen
$\large b \neq 0$
- Wenn $\large b = 0 $, ergibt die Funktion in allen Fällen 0, da sie mit 0 multipliziert wird

Wenn man eine Exponentialfunktion als Grafik zeichnet, ergibt sich eine steil ansteigende oder abfallende Kurve.

$\large a$ wird Wachstumsfaktor genannt und gibt an, wie schnell die Kurve wächst
$\large b$ gibt an, wo die Kurve die y-Achse schneidet

Die Grafik liegt immer auf einer Seite der x-Achse.

Die x-Achse fungiert als Asymptote, was bedeutet, dass sich die Kurve der Achse nähern, sie aber nie schneiden kann.

$\large a$ wird Wachstumsfaktor genannt:

$\large b$ gibt an, dass die Kurve die y-Achse bei $\large (0,b)$ schneidet

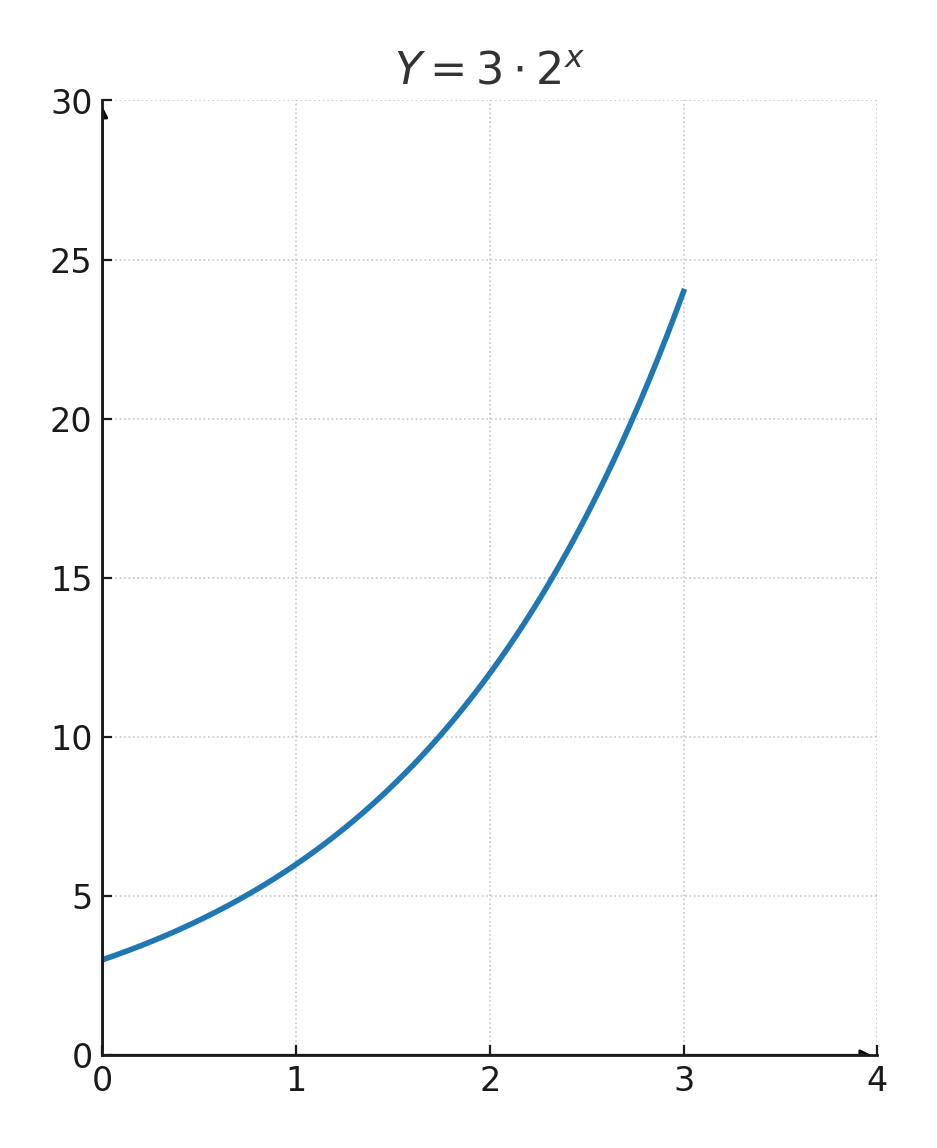
Betrachten wir diese Funktion:

$$ \large y=3 \cdot 2^x $$

Wir erkennen, dass es eine steigende Kurve ist, da $\large a=2$

Wir erkennen auch, dass sie die y-Achse bei $(0,3)$ schneidet

Wir probieren die Funktion $\large y=3 \cdot 2^x$

$\large x$	1	2	3
$\large y$	6	12	24

Exponentialfunktion

\(\large x\)	1	2	3
\(\large y\)	6	12	24