Funktionen

Eine Funktion wird verwendet, um einen Zusammenhang zwischen Dingen zu beschreiben. Wenn sich eine Sache ändert, ändert sich auch eine andere.

 

Wenn du ein Eis aus dem Gefrierschrank nimmst und es liegen lässt, schmilzt es langsam mit der Zeit, weil es wärmer wird.
Es gibt also einen Zusammenhang zwischen der vergehenden Zeit und der steigenden Temperatur.

 

Es könnte auch der Preis für Eis sein. Wenn du ein Eis kaufst, kostet es 5 Kronen. Wenn du zwei kaufst, kosten sie 10 Kronen, und so weiter.

Eine Funktion, die den Preis für Eis berechnen kann, sieht so aus:

 

$$ \large y=5x $$

 

Wobei \(\large x\) die Anzahl der Eise ist, und \(\large y \) der Preis.

 

Dieser Funktionstyp wird eine proportionale Funktion genannt.

Die Grafik einer proportionalen Funktion verläuft immer durch den Ursprung (den Punkt \((0,0)\)).

 

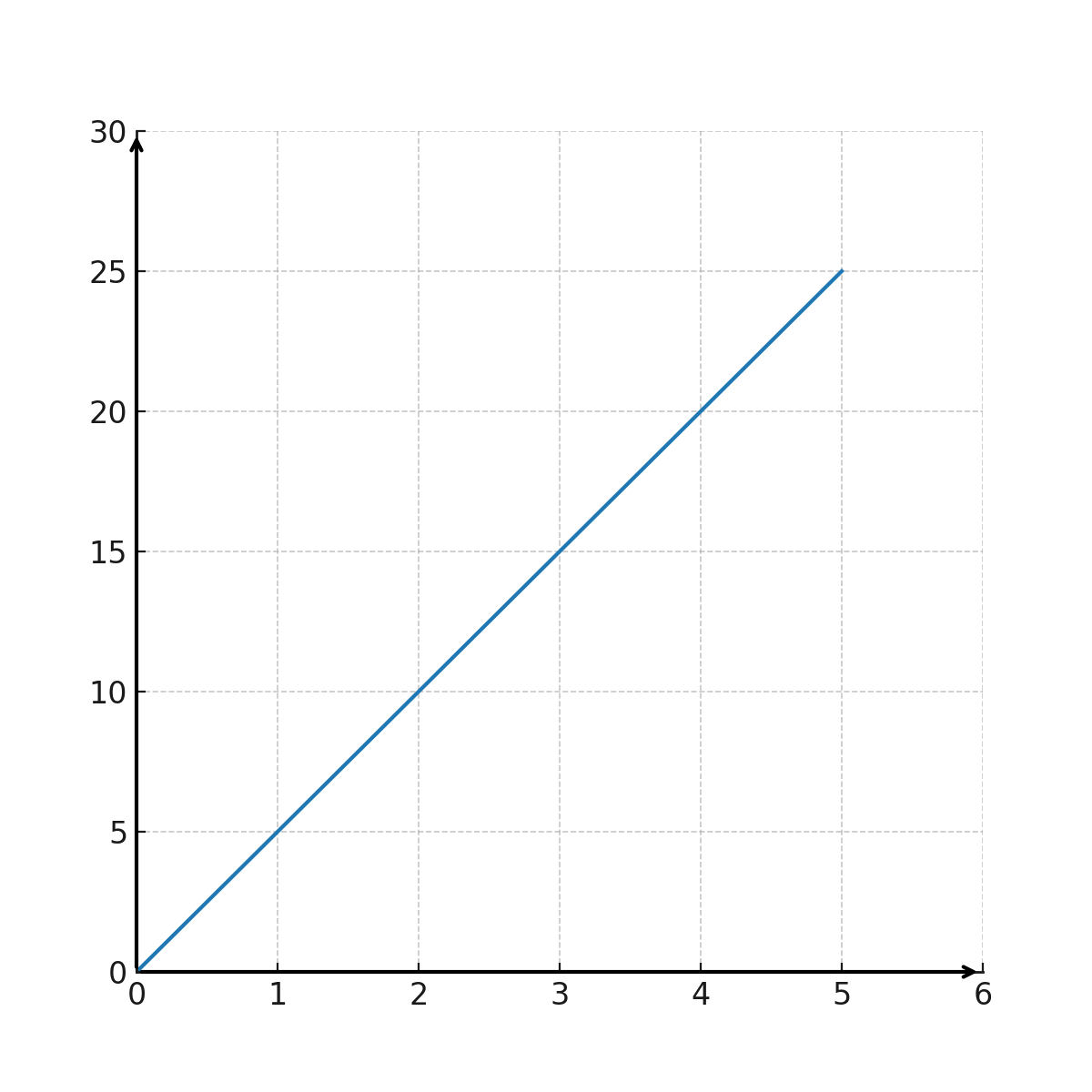
Die Grafik zeigt die Entwicklung des Preises für Eis

Anzahl der Eise auf der X Achse und der Preis auf der Y Achse

 

Eine Grafik zeichnen

Wenn man die Funktion als Grafik in einem Koordinatensystem zeichnet, nennt man \(\large x\) die unabhängige Variable (Anzahl der Eise), und \(\large y\) die abhängige Variable (der Preis).

Jedes Mal, wenn du einen Wert für \(\large x\) in deine Funktion einsetzt, kannst du den entsprechenden Wert für \(\large y\) berechnen und so einen Punkt im Koordinatensystem eintragen.

 

Beispiel:

• Wenn du \(\large x=1 \) Eis in die Funktion einsetzt, erhältst du \(\large y=5 \).

• Wenn du \(\large x=5 \) Eise in die Funktion einsetzt, erhältst du \(\large y=25\).

 

Nun haben wir zwei Koordinatensätze \(\large (1,5)\) und \(\large (5,25)\). Wenn sie im Koordinatensystem eingetragen und durch eine gerade Linie durch den Ursprung verbunden werden, erhalten wir die obige Grafik.