Fonction puissance

Une fonction puissance est une fonction où la variable $\large x$ apparaît comme base avec un exposant fixe.

Elle s’écrit sous cette forme :

$$ \large f(x)=k \cdot x^a $$

Il y a certaines conditions pour $\large k$ et $\large a$ :

$\large k \neq 0$
- Si $\large k = 0$, la fonction donnera toujours 0 dans tous les cas, car on multiplie par 0
$\large a$ peut être un entier, une fraction ou un nombre négatif
- Si $\large a$ est un entier positif, on obtient une courbe polynomiale croissante
- Si $\large a$ est une fraction, on obtient une fonction racine
- Si $\large a$ est négatif, on obtient une courbe décroissante semblable à une proportion inverse

Si l’on trace une fonction puissance en graphique, elle peut avoir des formes très différentes selon l’exposant $\large a$.

$\large a$ détermine la forme et la symétrie de la courbe
$\large k$ détermine la pente de la courbe et si elle s’oriente vers le haut ou vers le bas

La courbe peut couper l’axe des ordonnées à l’origine, sauf si une constante est ajoutée.

$\large a$ est appelé l’exposant :

Si $\large a$ est pair, la courbe ressemblera à une parabole et sera toujours du même côté de l’axe des x
Si $\large a$ est impair, la courbe passera par l’origine et aura des signes différents dans les deux branches

$\large k$ indique à quelle vitesse la courbe monte ou descend

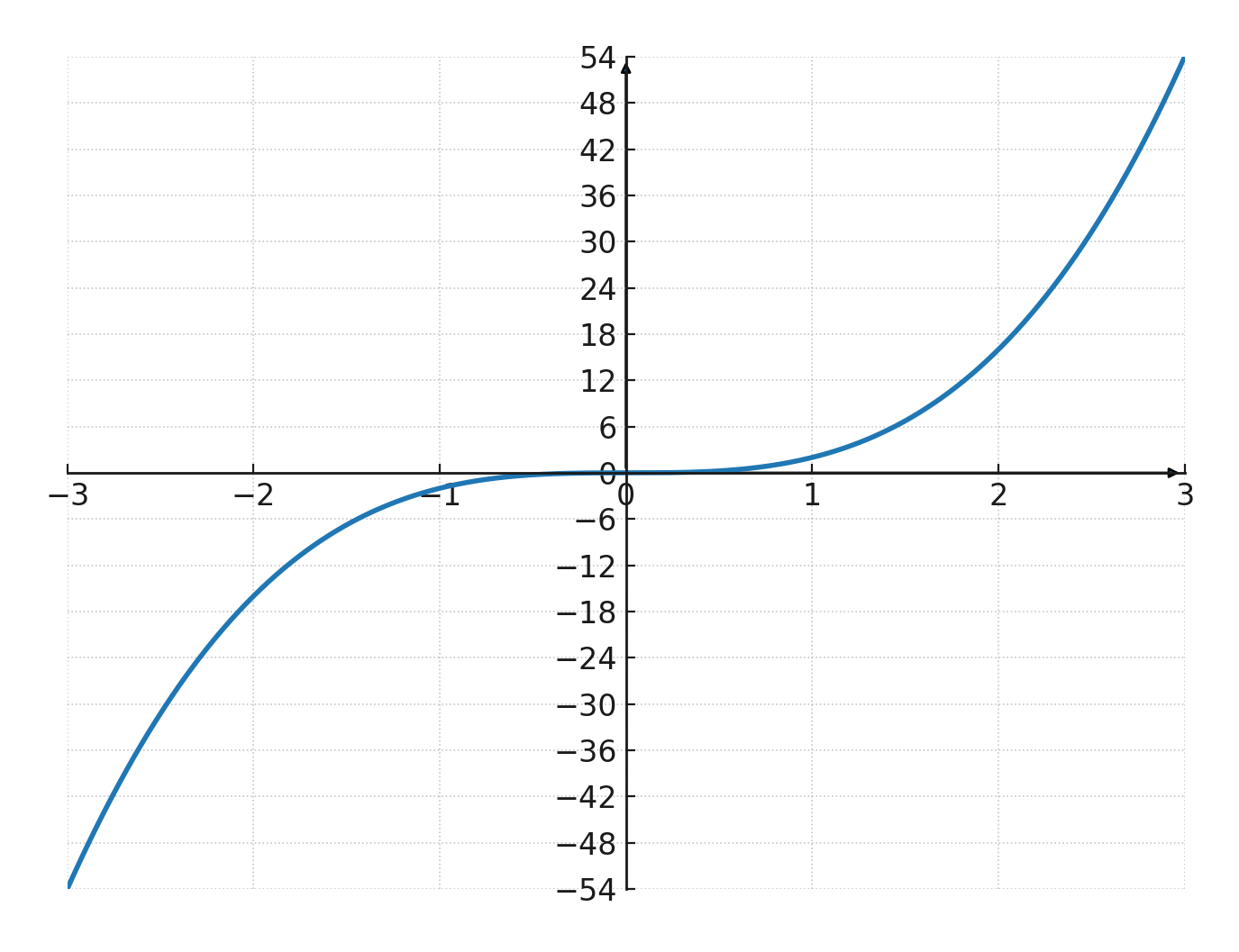
Si nous regardons cette fonction :

$$ \large y=2 \cdot x^3 $$

Nous pouvons voir qu’il s’agit d’une fonction puissance avec $\large a=3$, ce qui signifie que la courbe passe par l’origine et est impaire.

Nous pouvons également voir qu’elle croît rapidement, car $\large k=2$ la rend plus raide que la courbe standard $x^3$.

Essayons la fonction $\large y=2 \cdot x^3$

$\Large x$	-1	-2	-3	1	2	3
$\Large y$	-2	-16	-54	2	16	54

Fonction puissance

\(\Large x\)	-1	-2	-3	1	2	3
\(\Large y\)	-2	-16	-54	2	16	54