Fonction logarithmique
Une fonction logarithmique est l’inverse d’une fonction exponentielle. Elle décrit le nombre auquel une base donnée doit être élevée pour obtenir \(\large x\).
Elle s’écrit sous la forme :
$$ \Large f(x)=\log_a(x) $$
Il y a certaines conditions pour \(\large a\) et pour \(\large x\) :
- \(\large a>0\) et \(\large a \neq 1\)
- La base ne peut pas être 1, sinon le logarithme n’a aucune variation
- \(\large x>0\)
- Le logarithme est seulement défini pour des valeurs positives de \(\large x\)
Quand on trace une fonction logarithmique, on obtient une courbe qui croît ou décroît lentement selon la base.
- Si \(\large a>1\) la fonction est croissante
- Si \(\large 0
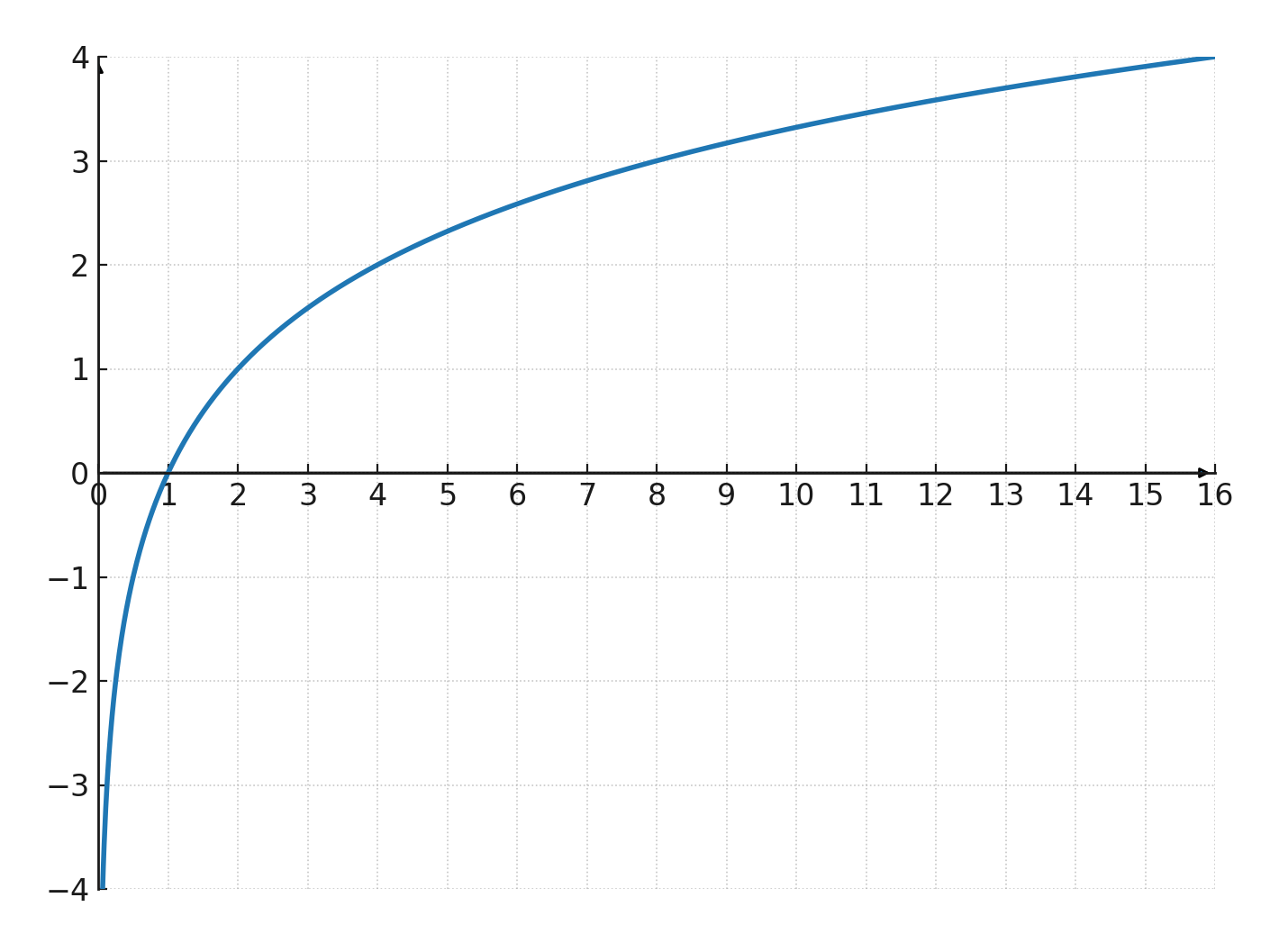
Le graphe a une asymptote verticale en \(\large x=0\). Il coupe l’axe des abscisses en \(\large (1,0)\). Il ne coupe pas l’axe des ordonnées, car la fonction n’est pas définie pour \(\large x\le 0\).
Base et caractéristiques
\(\large a\) est appelée la base :
- La base détermine si la courbe est croissante ou décroissante
- Changer la base étire ou comprime la courbe horizontalement
Le logarithme satisfait aussi la règle de changement de base et les règles de produit, mais ici nous nous concentrons sur la forme de la courbe.
Si nous regardons cette fonction :
$$ \Large y=\log_2(x) $$
La courbe est croissante, car \(\large a=2\) est supérieur à 1. Elle passe par \(\large (1,0)\) et a une asymptote verticale en \(\large x=0\).
Exemple
Essayons la fonction \(\large y=\log_2(x)\)
| \(\Large x\) | 0.25 | 0.5 | 1 | 2 | 4 |
| \(\Large y\) | -2 | -1 | 0 | 1 | 2 |