Fonction quadratique
Alors qu’une fonction linéaire est une fonction du premier degré, une fonction quadratique est une fonction du second degré et s’écrit sous cette forme :
$$ \large f(x)=a \cdot x^2 + b \cdot x + c $$
\(\large a\) ne peut pas être 0. Si l’on met 0 et que l’on multiplie, il ne reste rien. Le terme disparaît et il reste une fonction linéaire
Si tu représentes une fonction quadratique par un graphique, elle devient une parabole, pour laquelle les règles suivantes s’appliquent :
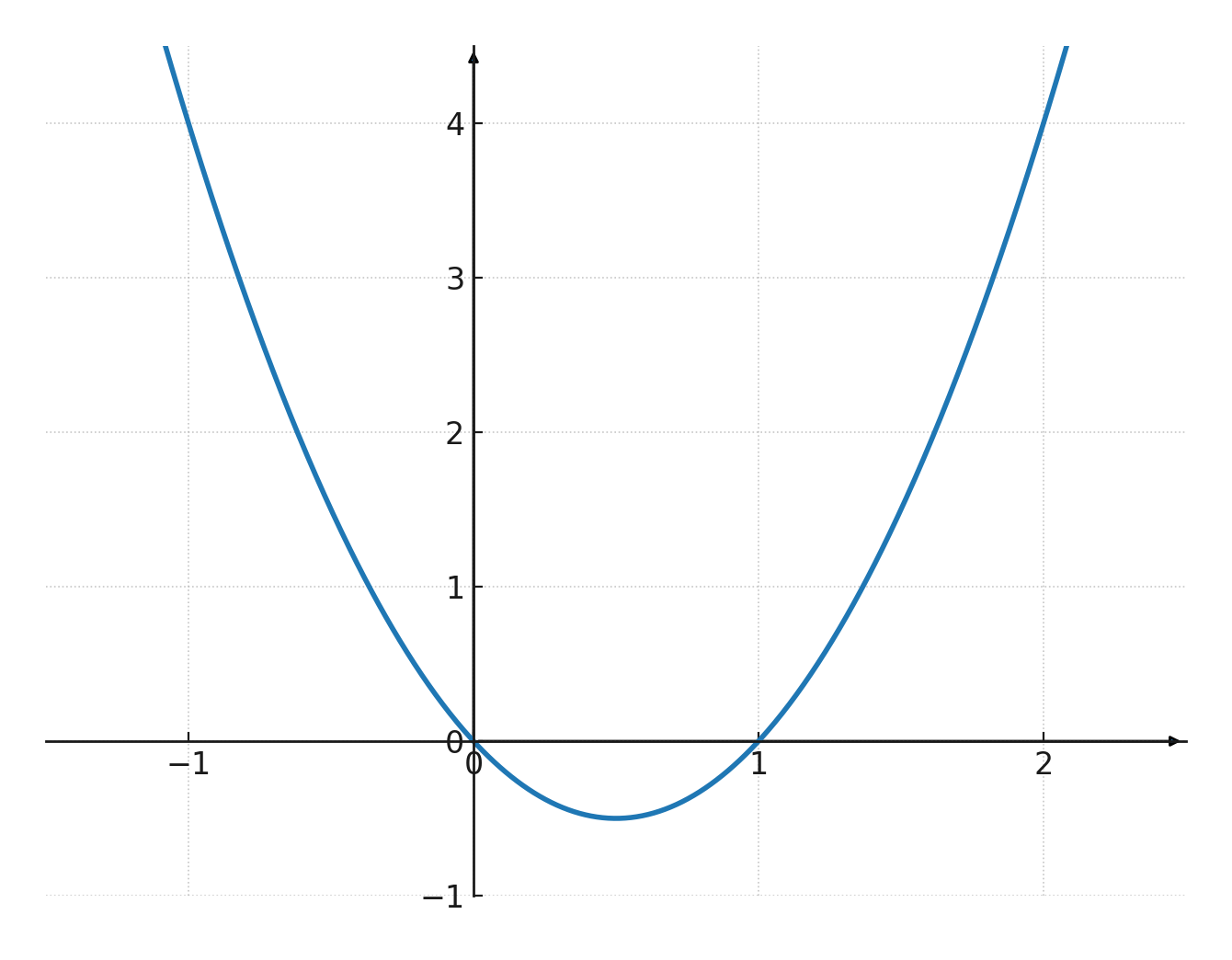
- Si \(\large a>0\) les branches pointent vers le haut
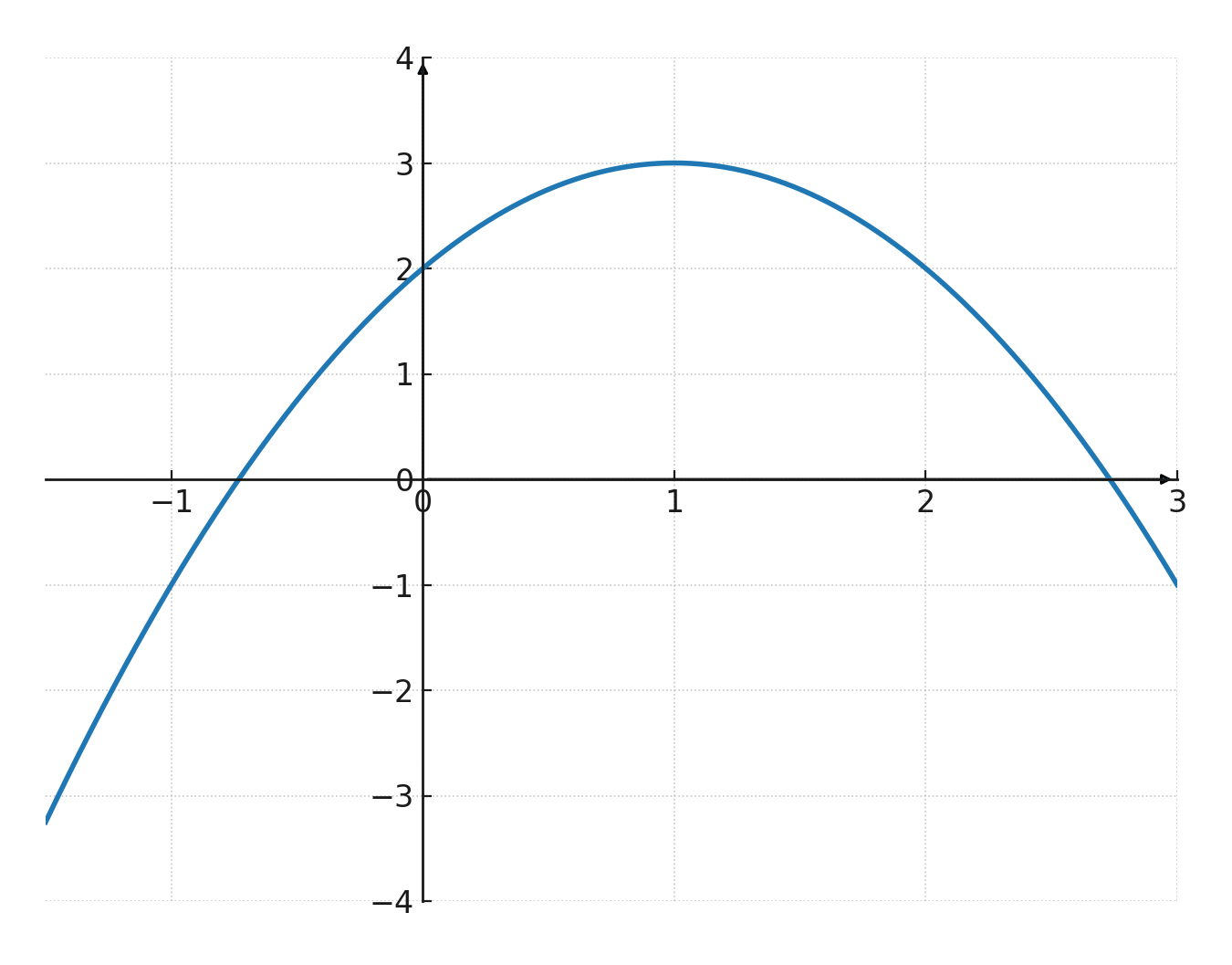
- Si \(\large a<0\) les branches pointent vers le bas
- La parabole coupe toujours l’axe y en \(\large (0,c) \)
- \(\large a \) détermine la raideur de la parabole, plus \(\large a \) est grand, plus la parabole est étroite
- La parabole est toujours symétrique par rapport à une droite verticale passant par le sommet (l’axe de symétrie)
Sommet et point d’intersection
Une fonction quadratique est liée aux équations du second degré.
Pour trouver l’intersection avec l’axe des x, tu dois résoudre l’équation du second degré où \( y=0\) :
$$ \large 0=ax^2+bx+c $$
Tu dois faire comme d’habitude lorsque tu résous des équations du second degré.
Le discriminant te dira quelque chose sur l’intersection de la parabole :
- Si \( D > 0\) elle coupe l’axe des x en deux points
- Si \( D < 0\) elle ne coupe pas l’axe des x
- Si \( D = 0\) elle coupe l’axe des x une seule fois
Pour calculer le sommet d’une parabole, nous utilisons aussi le discriminant :
$$ \large D= b^2-4ac $$
Lorsque nous avons le discriminant, nous pouvons calculer \((\large x,y)\) pour le sommet :
$$ \large x=\frac{-b}{2a} $$
$$ \large y=\frac{-D}{4a} $$
Exemple intersection
Essayons la fonction \(\large y=2x^2-2x+0\)
D’abord, trouvons le discriminant :
$$ D=b^2-4ac \Leftrightarrow $$
$$ D=2^2-4 \cdot 2 \cdot 0 \Leftrightarrow $$
$$ D=4 $$
Le discriminant est positif.
Cela signifie que la parabole coupera l’axe des x en deux points. Calculons ces deux points avec la formule quadratique :
$$ \Large x= \frac{-b \pm \sqrt{d}}{2 \cdot a} $$
Intersection 1 :
$$ \large x= \frac{-(-2) + \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2+2}{4} $$
$$ \large \underline{\underline{x= 1}} $$
Intersection 2 :
$$ \large x= \frac{-(-2) - \sqrt{4}}{2 \cdot 2} $$
$$ \large x= \frac{2-2}{4} $$
$$ \large \underline{\underline{x= 0}} $$
Exemple sommet
Dans l’exemple, nous avons trouvé que le discriminant est 4
Nous pouvons maintenant calculer \((x,y)\) pour le sommet :
$$ \large x=\frac{-b}{2a} \Leftrightarrow $$
$$ \large x=\frac{-(-2)}{2\cdot 2} \Leftrightarrow $$
$$ \large x=0,5 $$
$$ \large y=\frac{-D}{4a} \Leftrightarrow $$
$$ \large y=\frac{-4}{4 \cdot 2} \Leftrightarrow $$
$$ \large y=-0,5 $$
Sommet = \((0,5, -0,5)\)
Ensembles de coordonnées
Nous avons maintenant trois ensembles de coordonnées, les deux intersections et le sommet :
$$ \large (0,0), (0,5, -0,5), (0,1) $$
On pourrait tracer la parabole avec ces trois points, mais trouvons-en deux de plus en insérant -1 et 2 dans la fonction :
$$ \large y=2 \cdot -1^2-2 \cdot -1+0 $$
$$ \large y=4 $$
$$ \large y=2 \cdot 2^2-2 \cdot 2+0 $$
$$ \large y=4 $$
| \(x\) | 0 | 0,5 | 0 | -1 | 2 |
| \(y\) | 0 | -0,5 | 1 | 4 | 4 |
On peut maintenant la tracer.