Fonction exponentielle

Une fonction exponentielle est une fonction où la variable $\large x$ se trouve dans l’exposant.

Elle s’écrit sous cette forme :

$$ \large f(x)=b \cdot a^x $$

Il y a certaines conditions pour $\large a$ et $\large b$ :

$\large a > 0$ et $\large a \neq 1$
- Si $\large a = 1 $, la fonction devient constante sans évolution
- Si $\large a \le 0$, la fonction ne peut pas être calculée pour tous les nombres réels, mais seulement pour les entiers
$\large b \neq 0$
- Si $\large b = 0 $, la fonction donnera toujours 0 dans tous les cas, car elle est multipliée par 0

Si l’on trace une fonction exponentielle sous forme de graphique, elle sera une courbe raide croissante ou décroissante.

$\large a$ est appelé facteur de croissance et indique la vitesse de croissance de la courbe
$\large b$ indique où la courbe coupe l’axe y

La courbe sera toujours située d’un seul côté de l’axe x.

L’axe x fonctionne comme une asymptote, ce qui signifie que la courbe peut s’en approcher mais ne jamais le couper.

$\large a$ est appelé le facteur de croissance :

$\large b$ indique que la courbe coupera l’axe y en $\large (0,b)$

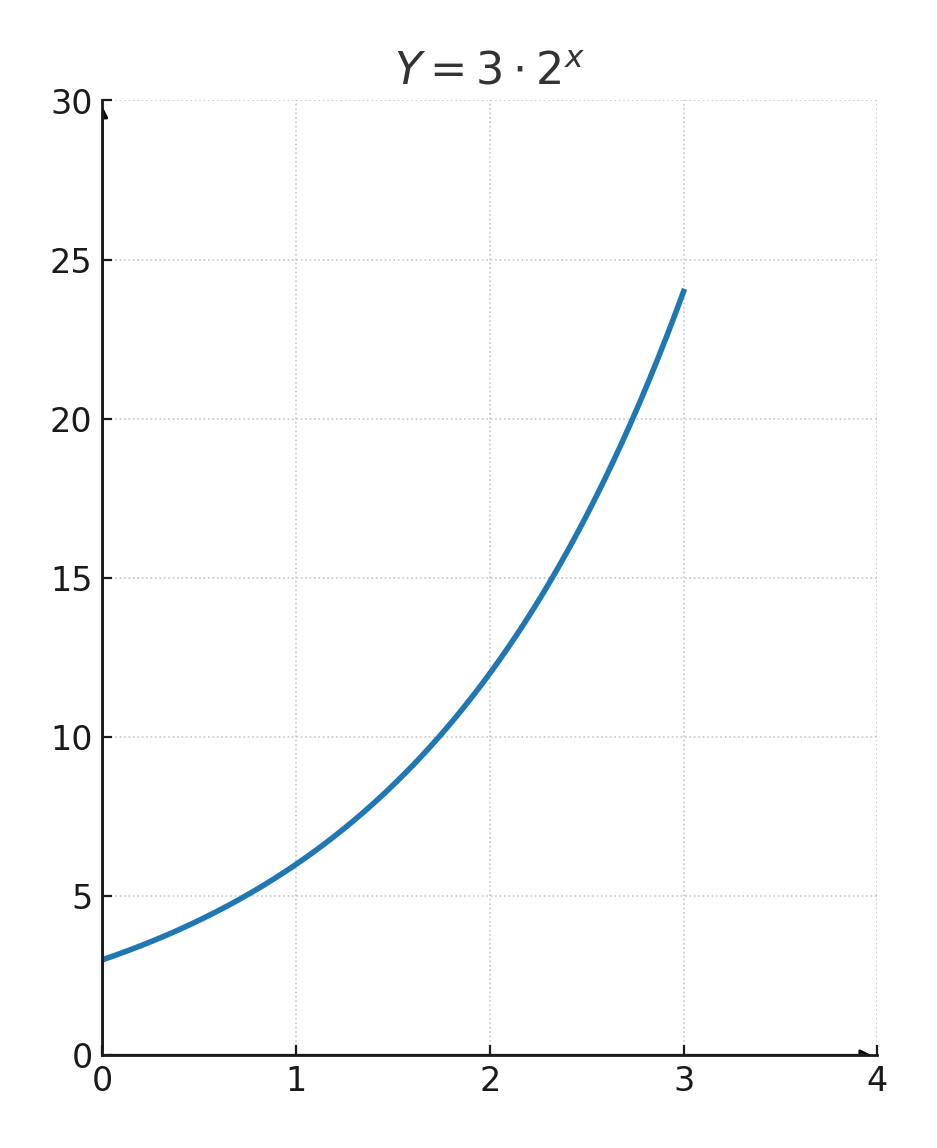
Si l’on observe cette fonction :

$$ \large y=3 \cdot 2^x $$

On voit que c’est une courbe croissante, car $\large a=2$

On voit aussi qu’elle coupe l’axe y en $(0,3)$

Essayons la fonction $\large y=3 \cdot 2^x$

$\large x$	1	2	3
$\large y$	6	12	24

Fonction exponentielle

\(\large x\)	1	2	3
\(\large y\)	6	12	24