Fonction linéaire

Une fonction linéaire s’écrit sous cette forme :

$$ \large f(x)=a \cdot x + b $$

Si une fonction linéaire est tracée comme une courbe, elle sera toujours une droite.

La courbe peut être croissante, décroissante ou horizontale selon $ \large a$, et $ \large b$ indique où elle coupe l’axe des y

$ \large a$ s’appelle la pente :

Si $ \large a > 0$ la droite est croissante de gauche à droite
Si $ \large a < 0$ la droite est décroissante de gauche à droite
Si $ \large a = 0$ la droite est horizontale, car quel que soit $\large x$, $\large y$ reste toujours le même.

$ \large b$ indique que la droite coupe l’axe des y au point $(0,b)$

Si nous regardons cette fonction :

$$ \large y=2x+5 $$

Nous voyons qu’il s’agit d’une droite croissante, car $\large a=2$.

Nous voyons aussi qu’elle coupe l’axe des y en $(0,5)$, car $\large b=5$.

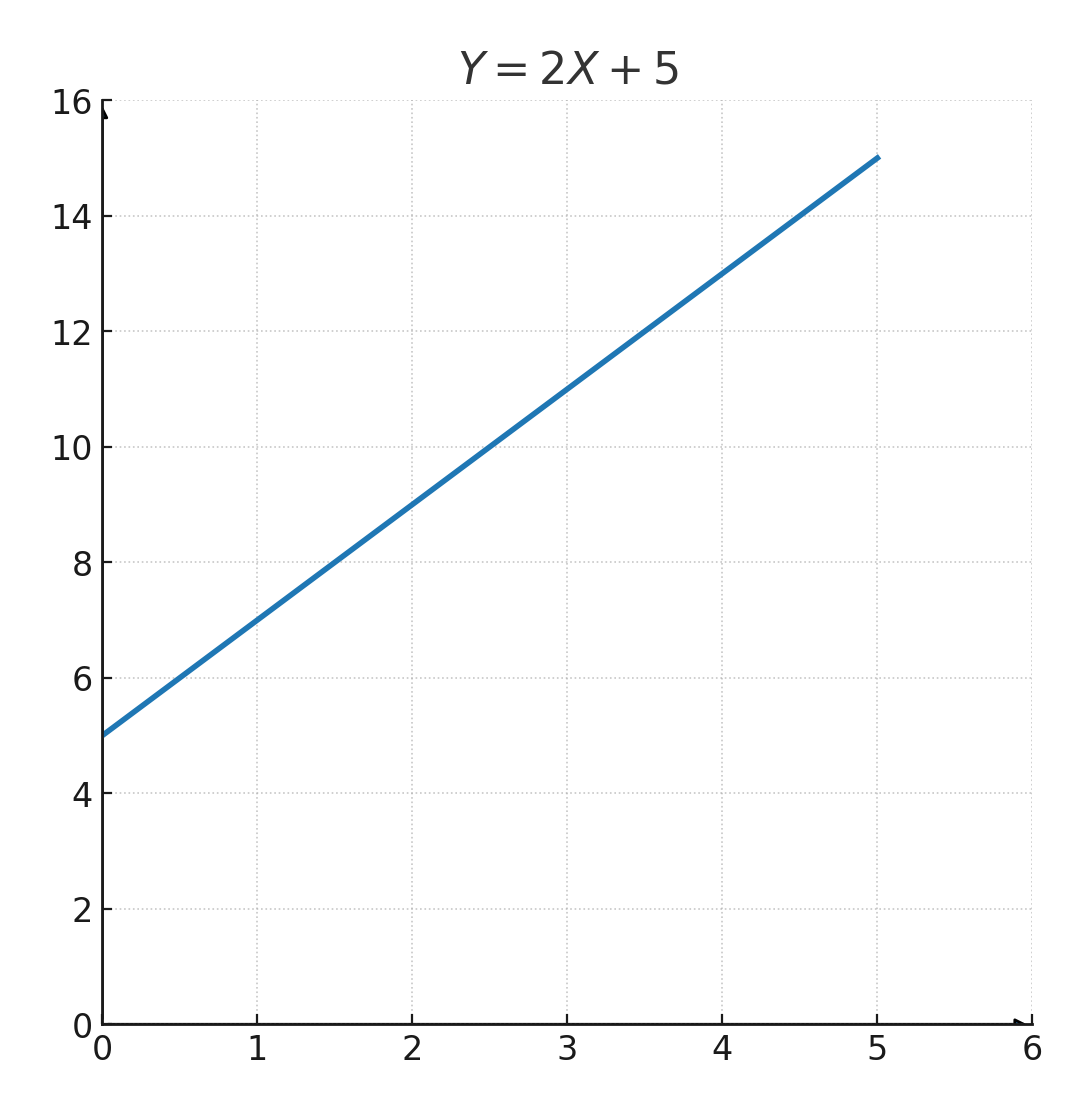
Essayons la fonction : $ \large y=2x+5 $

Les coordonnées sont placées dans le tableau de valeurs ci-dessous puis dans le système de coordonnées, afin que la courbe puisse être tracée :

$\large x$	1	2	3	4	5
$\large y$	7	9	11	13	15

Fonction linéaire

Si nous avons les coordonnées $(2,9)$ et $(4,13)$, il est possible de trouver $\large a$ et $\large b$ de la manière suivante :

$$ \large a = \frac{y_2-y_1}{x_2-x_1} \Leftrightarrow $$

$$ \large a = \frac{13-9}{4-2} \Leftrightarrow $$

$$ \large a = \frac{4}{2} \Leftrightarrow $$

$$ \large a = 2 $$

Quand nous avons trouvé $\large a$, nous pouvons aussi trouver $\large b$ avec l’une de ces deux formules. (Peu importe laquelle on utilise)

$$ \large b = y_1 - a \cdot x_1 $$

$$ \large b = y_2 - a \cdot x_2 $$

Nous utilisons la première :

$$ \large b = 9 - 2 \cdot 2 \Leftrightarrow $$

$$ \large b = 9 - 4 \Leftrightarrow $$

$$ \large b = 5 $$

La formule de la fonction pour les coordonnées $(2,9)$ et $(4,13)$ est donc :

$$ \large y = ax + b $$

$$ \large y = 2x + 5 $$

\(\large x\)	1	2	3	4	5
\(\large y\)	7	9	11	13	15