Fonctions

Une fonction est utilisée pour décrire une relation entre des choses. Si une chose change, alors une autre change aussi.

 

Si tu sors une glace du congélateur et que tu la laisses, elle fondra lentement au fur et à mesure que le temps passe, parce qu’elle se réchauffe.
Il y a donc une relation entre le temps qui passe et la température qui augmente.

 

Cela pourrait aussi être le prix de la glace. Si tu achètes une glace, elle coûte 5 couronnes. Si tu en achètes deux, elles coûtent 10 couronnes, et ainsi de suite.

Une fonction qui peut calculer le prix de la glace ressemble à ceci :

 

$$ \large y=5x $$

 

Où \(\large x\) est le nombre de glaces, et \(\large y \) est le prix.

 

Ce type de fonction s’appelle une fonction proportionnelle.

La courbe d’une fonction proportionnelle passera toujours par l’origine (le point \((0,0)\)).

 

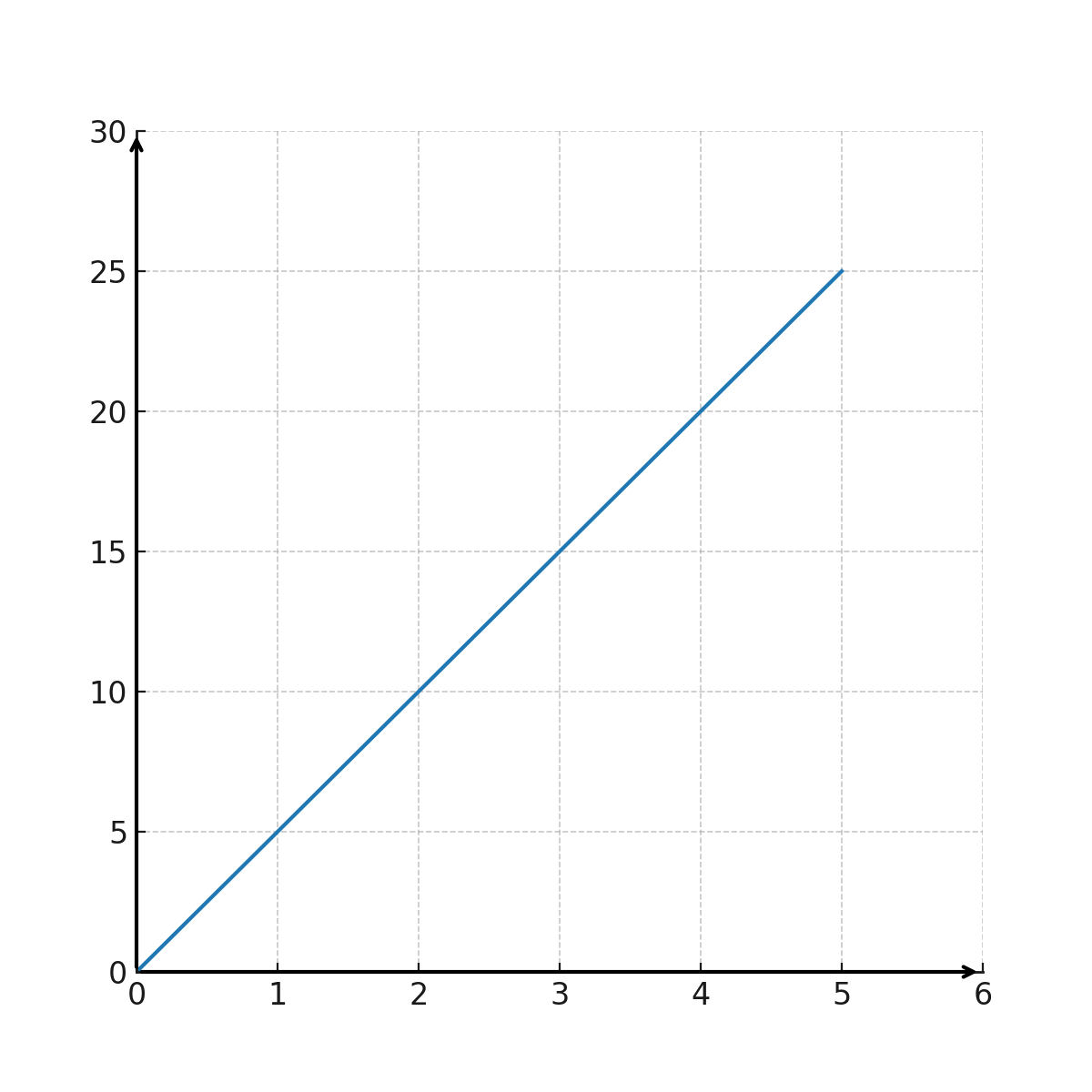
La courbe montre l’évolution du prix de la glace

Nombre de glaces sur l’axe X et le prix sur l’axe Y

 

Tracer une courbe

Lorsqu’on trace la fonction comme une courbe dans un système de coordonnées, \(\large x\) est appelée variable indépendante (nombre de glaces), et \(\large y\) variable dépendante (le prix).

Chaque fois que tu insères une valeur de \(\large x\) dans ta fonction, tu peux calculer la valeur correspondante de \(\large y\) et ainsi placer un point dans le système de coordonnées.

 

Exemple :

• Si tu insères \(\large x=1 \) glace dans la fonction, tu obtiens \(\large y=5 \).

• Si tu insères \(\large x=5 \) glaces dans la fonction, tu obtiens \(\large y=25\).

 

Nous avons maintenant deux ensembles de coordonnées \(\large (1,5)\) et \(\large (5,25)\). Lorsqu’ils sont placés dans le système de coordonnées et reliés par une ligne droite passant par l’origine, nous obtenons la courbe ci-dessus.