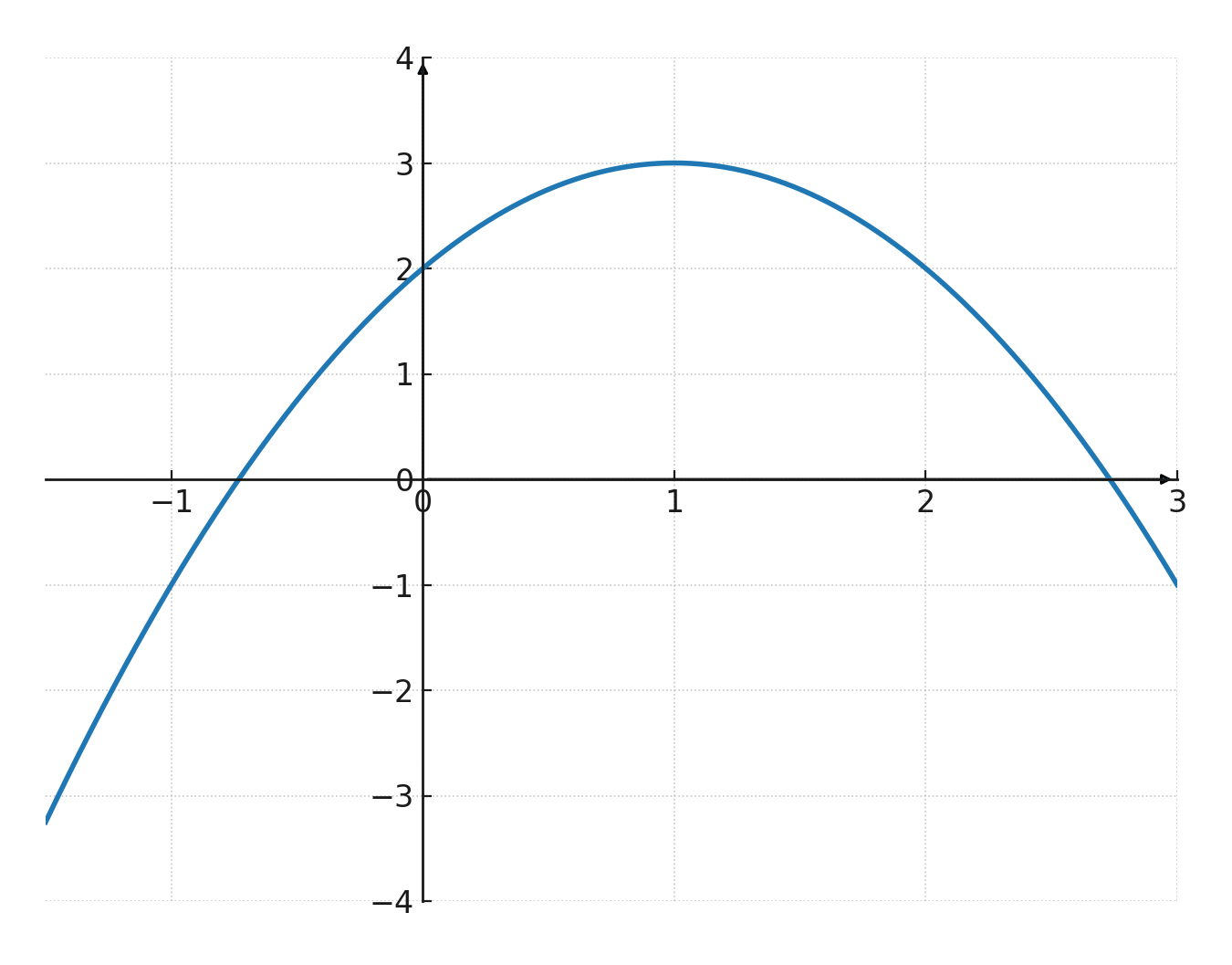
Función cuadrática

Donde una función lineal es una función de primer grado, una función cuadrática es una función de segundo grado y se escribe en esta forma:

 

$$ \large f(x)=a \cdot x^2 + b \cdot x + c $$

 

\(\large a\) no puede ser 0. Si ponemos 0 y multiplicamos, no queda nada. El término desaparece y lo que queda es una función lineal

 

Si dibujas una función cuadrática como gráfica, se convierte en una parábola, donde se cumple lo siguiente:

 

• Si \(\large a>0\) los brazos apuntan hacia arriba
• Si \(\large a<0\) los brazos apuntan hacia abajo  
• La parábola siempre corta el eje y en \(\large (0,c) \)
• \(\large a \) determina cuán inclinada es la parábola, cuanto mayor es \(\large a \), más estrecha se vuelve
• La parábola siempre es simétrica respecto a una línea vertical que pasa por el vértice (el eje de simetría)

 

 

Vértice e intersección

Una función cuadrática está relacionada con las ecuaciones cuadráticas.

Para encontrar la intersección con el eje x, debes resolver la ecuación cuadrática donde \( y=0\):

 

$$ \large 0=ax^2+bx+c $$

 

Debes hacer como siempre al resolver ecuaciones cuadráticas.

El discriminante te dirá un poco sobre la intersección de la parábola:

 

• Si \( D > 0\) corta el eje x en dos lugares
• Si \( D < 0\) no corta el eje x
• Si \( D = 0\) corta el eje x solo una vez

 

Para calcular el vértice de una parábola, también usamos el discriminante:

 

$$ \large D= b^2-4ac $$

 

Cuando tenemos el discriminante, podemos calcular \((\large x,y)\) para el vértice:

 

$$ \large x=\frac{-b}{2a} $$

$$ \large y=\frac{-D}{4a} $$

 

Ejemplo intersección

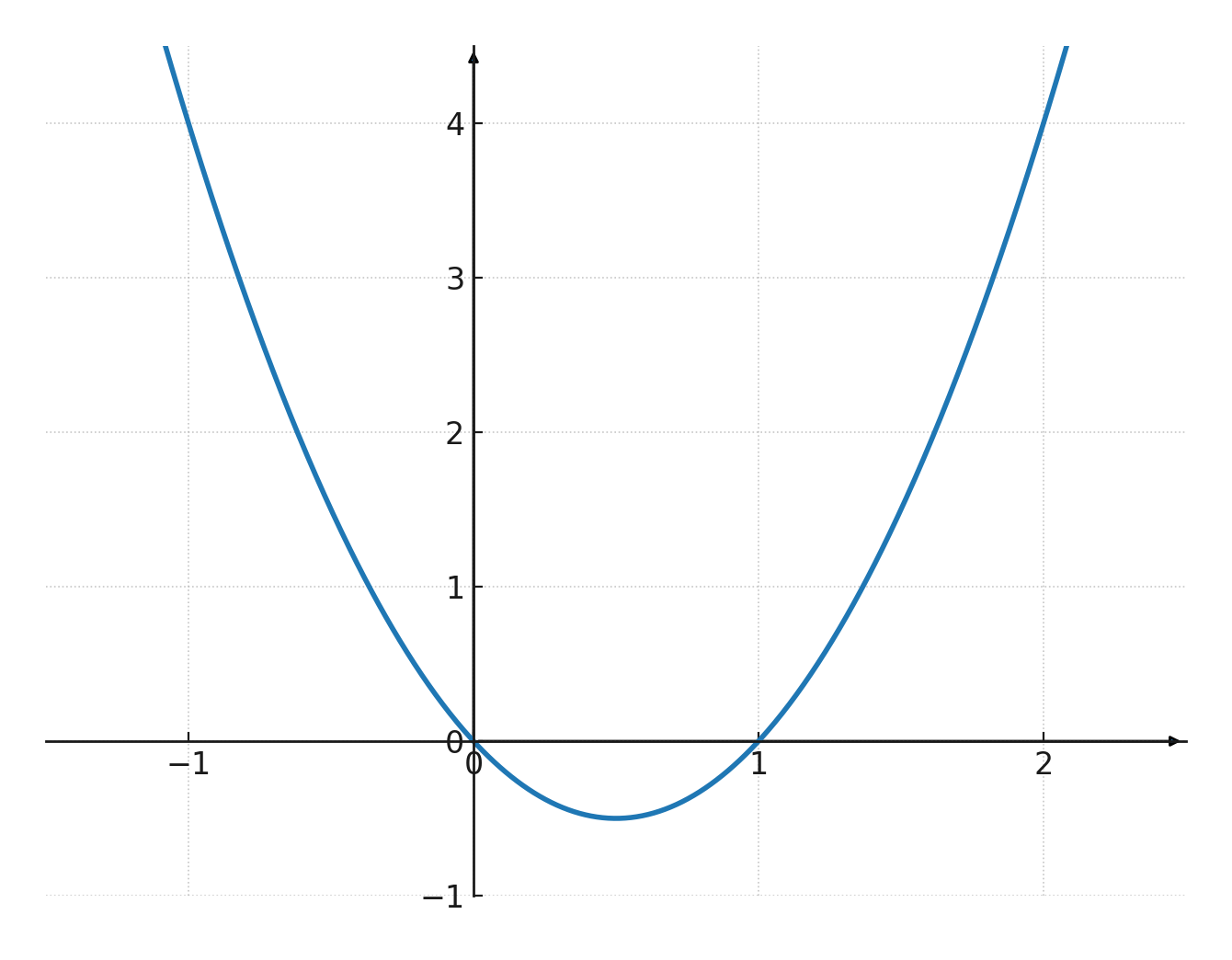
Probamos la función \(\large y=2x^2-2x+0\)

Primero encontramos el discriminante:

 

$$ D=b^2-4ac \Leftrightarrow $$

$$ D=2^2-4 \cdot 2 \cdot 0 \Leftrightarrow $$

$$ D=4 $$

 

El discriminante es positivo.

Esto significa que la parábola cortará el eje x en dos lugares. Calculamos esos dos lugares con la fórmula cuadrática:

 

$$ \Large x= \frac{-b \pm \sqrt{d}}{2 \cdot a} $$

 

Intersección 1:

$$ \large x= \frac{-(-2) + \sqrt{4}}{2 \cdot 2} $$

$$ \large x= \frac{2+2}{4} $$

$$ \large \underline{\underline{x= 1}} $$

 

Intersección 2:

$$ \large x= \frac{-(-2) - \sqrt{4}}{2 \cdot 2} $$

$$ \large x= \frac{2-2}{4} $$

$$ \large \underline{\underline{x= 0}} $$

 

Ejemplo vértice

En el ejemplo vimos que el discriminante es 4

Ahora podemos calcular \((x,y)\) para el vértice:

 

$$ \large x=\frac{-b}{2a} \Leftrightarrow $$

$$  \large x=\frac{-(-2)}{2\cdot 2} \Leftrightarrow  $$

$$ \large x=0,5 $$

 

$$ \large y=\frac{-D}{4a} \Leftrightarrow $$

$$ \large y=\frac{-4}{4 \cdot 2} \Leftrightarrow $$

$$ \large y=-0,5 $$

 

Vértice = \((0,5, -0,5)\)

 

Conjuntos de coordenadas

Ahora tenemos tres conjuntos de coordenadas, las dos intersecciones y el vértice:

 

$$ \large (0,0), (0,5, -0,5), (0,1) $$

 

Podríamos dibujar la parábola con estos tres, pero vamos a encontrar dos más, insertando -1 y 2 en la función:

 

$$ \large y=2 \cdot -1^2-2 \cdot -1+0 $$

$$ \large y=4 $$

 

$$ \large y=2 \cdot 2^2-2 \cdot 2+0 $$

$$ \large y=4 $$

 

\(x\)	0	0,5	0	-1	2
\(y\)	0	-0,5	1	4	4

 

Ahora se puede dibujar.