Polinomios

Un polinomio es un tipo específico de función matemática, formado por términos donde una variable (normalmente llamada x) se eleva a diferentes potencias y se multiplica por números (coeficientes). Finalmente, se pueden sumar varios de estos términos.

 

El tipo más simple de polinomio es una función constante. Se llama polinomio de grado 0, porque no aparece ninguna x. La función siempre tiene el mismo valor, sin importar cuál sea x.

Un ejemplo es:

 

$$ \large f(x) = 5 $$

 

Aquí el valor siempre es 5, ya sea que x sea -10, 0 o 100. La gráfica es por lo tanto una línea horizontal paralela al eje x.

 

Aquí un ejemplo de un polinomio de 2º grado. También se llama una función cuadrática:

 

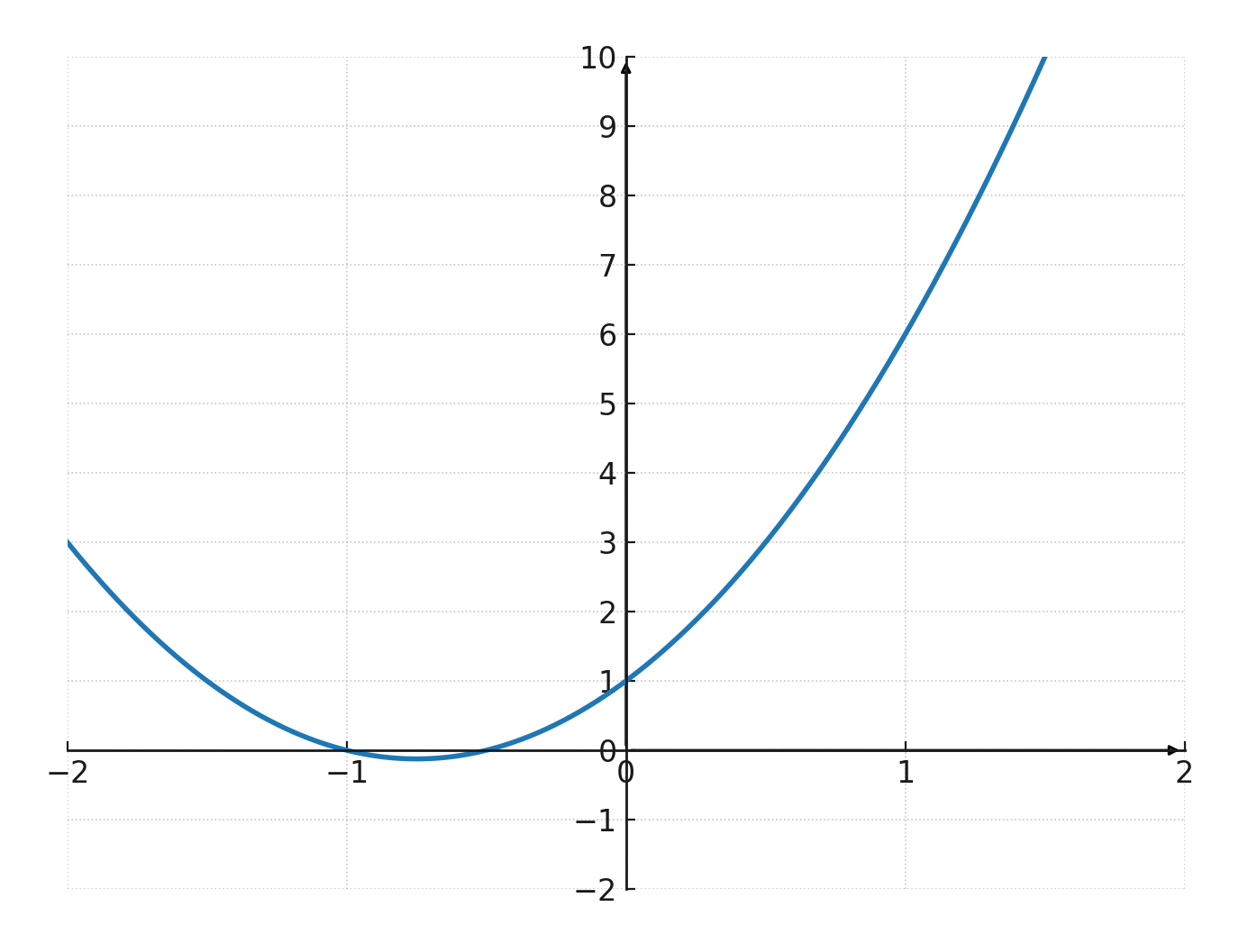
$$ \large f(x) = 2x^2 + 3x + 1 $$

 

Aquí hay tres términos: \(2x^2\), \(3x\) y \(1\). Si se dibuja como una gráfica, será una parábola:

 

 

 

El grado de un polinomio

El exponente más alto de x se llama el grado del polinomio:

 

• Grado 0: Función constante, p. ej. \( f(x)=5 \).
• Grado 1: Función lineal, p. ej. \( f(x)=2x+1 \).
• Grado 2: Función cuadrática, p. ej. \( f(x)=x^2-3x+2 \).
• Grado 3: Función cúbica, p. ej. \( f(x)=x^3-3x+2 \).

 

A partir del grado 4 en adelante, normalmente solo se usa el término polinomio de grado n en lugar de un nombre especial.

 

Cuanto mayor es el grado, más complejas se vuelven las gráficas y las curvas pueden doblarse de más maneras.

 

Una familia infinita

Los polinomios forman toda una familia de funciones.

Existen polinomios de todos los grados, y por lo tanto se puede decir que en principio es una secuencia infinita de funciones. Cada polinomio tiene su propia gráfica, dependiendo del grado y de los números usados como coeficientes.

 

¿Dónde se usan los polinomios?

Los polinomios son importantes porque aparecen en muchas áreas de la matemática y en la vida real:

 

• En economía, una función puede describir la evolución de un interés o inversión.
• En física, una función puede describir un movimiento o una velocidad.
• En estadística, ayudan a ajustar curvas a datos.

 

Aunque los polinomios suenen técnicos, son bloques de construcción fundamentales en matemáticas y nos dan herramientas para describir y comprender desde una simple línea recta hasta relaciones mucho más complejas.