Función cúbica

Una función cúbica es una función de tercer grado. La fórmula general es la siguiente:

$$ \large f(x) = a \cdot x^3 + b \cdot x^2 + c \cdot x + d $$

Aquí se cumple que $ \large a \neq 0$, de lo contrario se multiplicaría por 0 y la función se convertiría en una función cuadrática.

La gráfica de una función cúbica se llama curva cúbica. Normalmente tiene forma de S, pero puede variar dependiendo de los coeficientes.

Si $ \large a > 0$, la gráfica comienza en la esquina inferior izquierda y termina en la esquina superior derecha.
Si $ \large a < 0$, la gráfica comienza en la esquina superior izquierda y termina en la esquina inferior derecha.

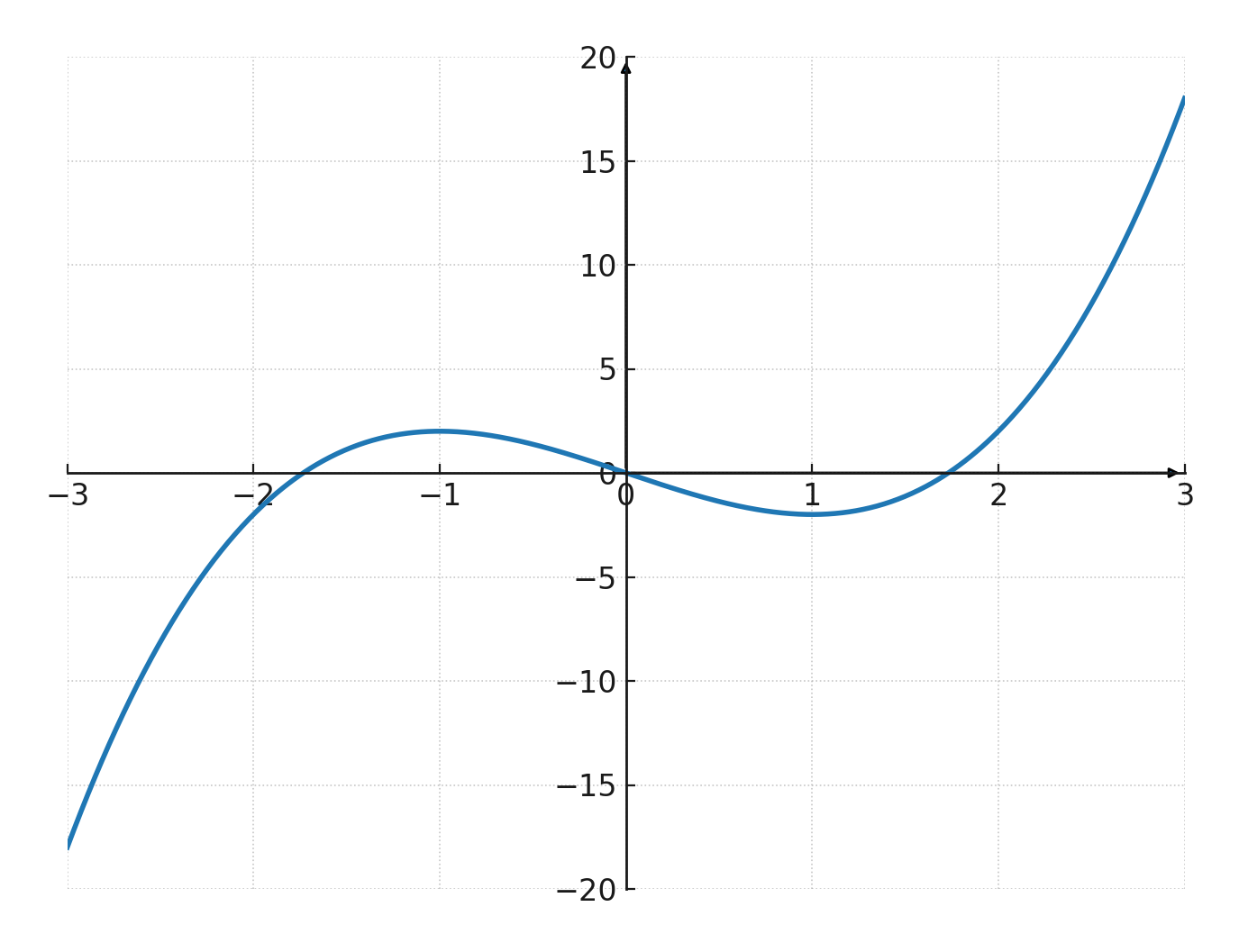
Función cúbica

Raíces

Una función cúbica puede tener una o tres intersecciones con el eje x, dependiendo del discriminante.

Una raíz es el punto donde corta o toca el eje x, es decir, donde $ \large f(x) = 0 $. Por lo tanto, siempre tiene al menos una raíz real y puede tener hasta tres raíces reales.

Puntos máximo y mínimo

Una función cúbica puede tener tanto un máximo local (punto máximo) como un mínimo local (punto mínimo), si el discriminante lo permite. En ese caso la gráfica toma su forma característica de S.

Si no se cumplen las condiciones, la gráfica simplemente subirá o bajará sin curvarse.

Otros puntos importantes

La gráfica corta el eje y en el punto $ \large (0,d)$
La gráfica siempre tiene un punto de inflexión en $ \large x=-\frac{b}{3a}$
Se puede determinar la forma de la gráfica a partir de la expresión $ \large b^2 - 3ac $
- Si $ \large b^2-3ac>0$, hay dos extremos (un máximo y un mínimo).
- Si $ \large b^2-3ac=0$, hay un punto estacionario doble.
- Si $ \large b^2-3ac<0$, no hay extremos.

Ejemplo

Probemos con esta función:

$$ \large f(x) = x^3 - 3x + 2 $$

Aquí $ \large a = 1$, $ \large b = 0$, $ \large c = -3$, $ \large d = 2$.

La función da el siguiente conjunto de coordenadas:

$ x $	-2	-1	0	1	2	3
$ y $	-4	4	2	0	4	20

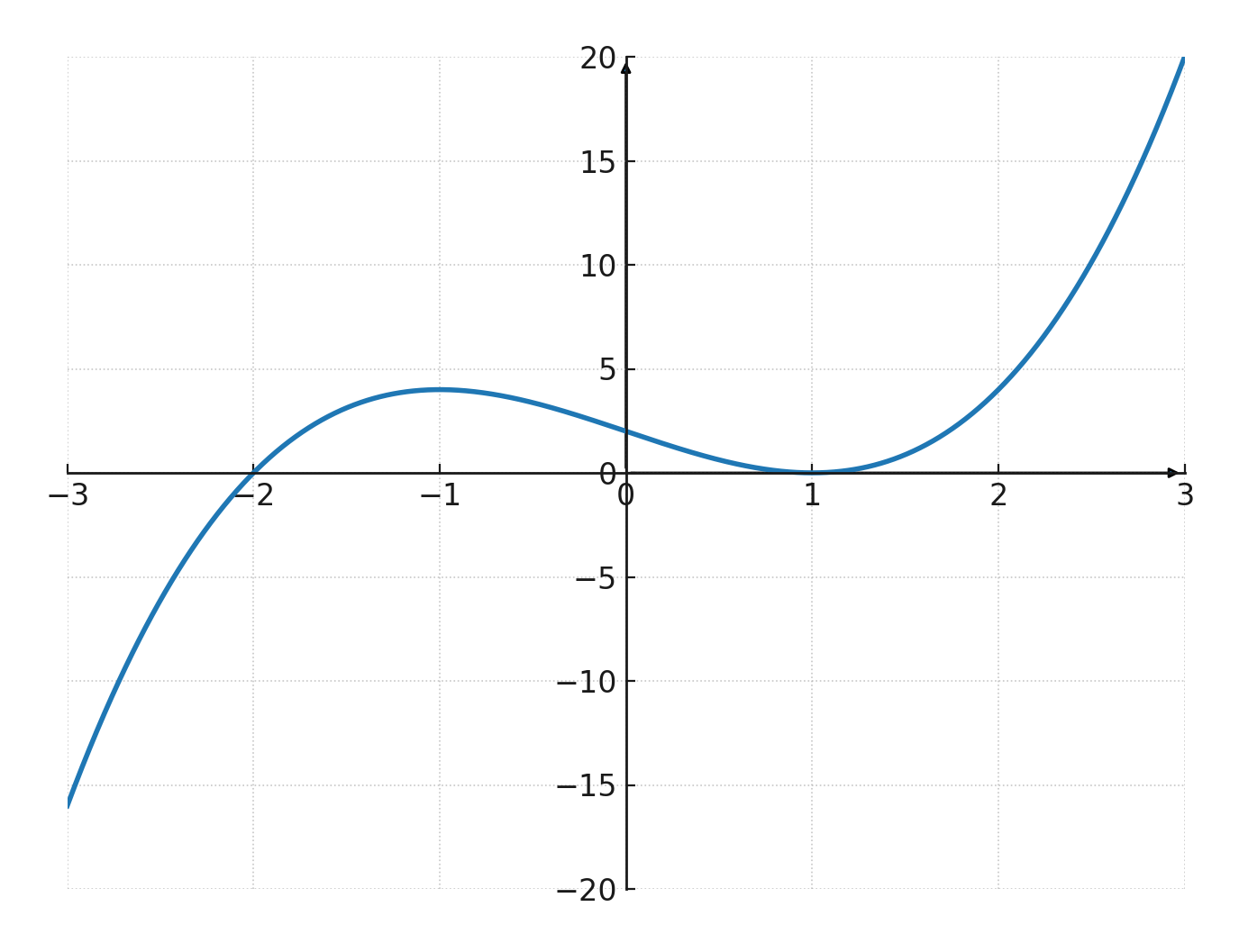
Ejemplo de función cúbica

Es posible factorizar la función:

$$ \large f(x) = (x+2)(x-1)^2 $$

Así la gráfica tiene las raíces $ \large (-2,0)$ y $ \large (1,0)$. El punto $ \large (1,0)$ es una raíz doble, lo que significa que la gráfica toca el eje x en ese punto sin cruzarlo.

Si en cambio lo hubiera cruzado, la función habría tenido tres raíces distintas.

La gráfica corta el eje y en el punto $ \large (0,2)$.

El discriminante da $ \large b^2 - 3ac = 0^2 - 3 \cdot 1 \cdot (-3) = 9 > 0$, por lo que la función tiene tanto un máximo local como un mínimo local. Por eso la gráfica toma la forma clásica de S.