Inscribed circle

In every triangle, a circle can be drawn that touches all three sides of the triangle.

 

This is called the inscribed circle.

 

 

 

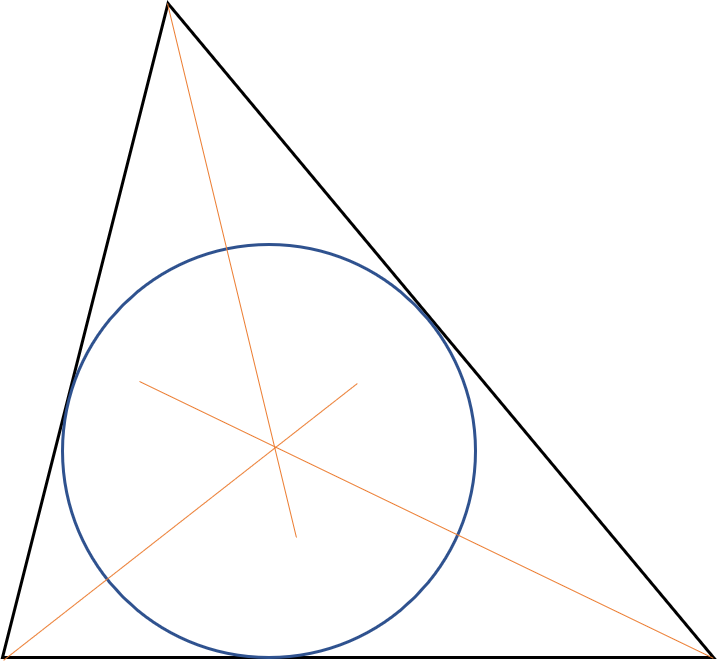
Angle bisectors and center

An angle bisector is a line that divides an angle into two equal parts.

The center of the circle is found by drawing angle bisectors in each of the triangle's three angles.

The intersection point of the angle bisectors is the center of the circle.

If an angle is 64 degrees, you must draw a line exactly in the middle, dividing the angle into two angles of 32 degrees each.

 

Radius and area

The radius of the circle can be calculated with this formula:

 

$$ \large r= \frac{2 \cdot A}{a+b+c} $$

 

Where \(\large A\) is the area of the triangle.

If you want to find the area of the triangle, you can rearrange the formula:

 

$$ \large A = \frac{r \cdot (a + b + c)}{2} $$