Circumscribed circle

In every triangle, a circle can be drawn that touches all three vertices of the triangle.

 

This is called the circumscribed circle.

 

 

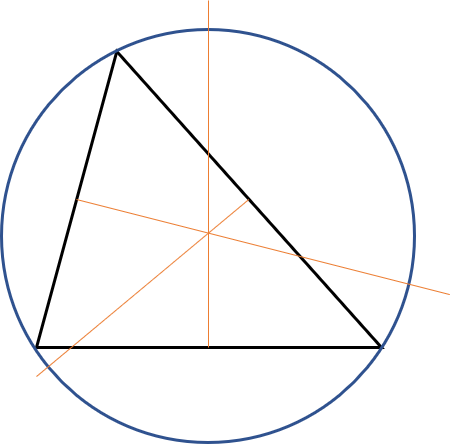
Perpendicular bisectors and center

A perpendicular bisector is a line that is perpendicular to a segment and divides it in the middle.

The perpendicular bisectors divide the three sides of the triangle (a, b, c) and intersect at the center of the circumscribed circle.

If you want to draw a circumscribed circle, start by drawing the three perpendicular bisectors. At their intersection point, place your compass and you can draw the circle.

 

Radius and area

The radius of the circumscribed circle can be calculated with this formula:

 

$$ \large r=\frac{a \cdot b \cdot c}{4 \cdot A} $$

 

Where \(\large A\) is the area of the triangle.

If you want to find the area of the triangle, you can rearrange the formula:

 

$$ \large A=\frac{a \cdot b \cdot c}{4 \cdot r} $$

 

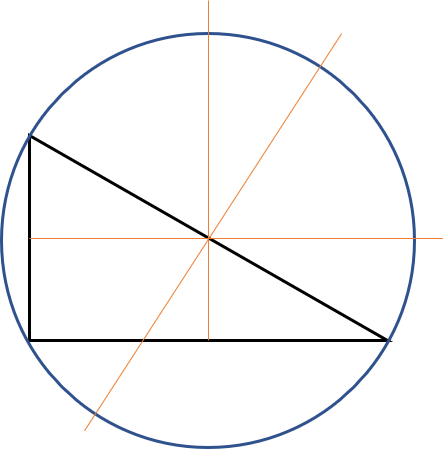
Right triangle

The circumscribed circle of a right triangle will always have its center exactly in the middle of the hypotenuse.

This also makes it easier to find the radius, which is half the length of side c:

 

$$ \large r=\frac{c}{2} $$