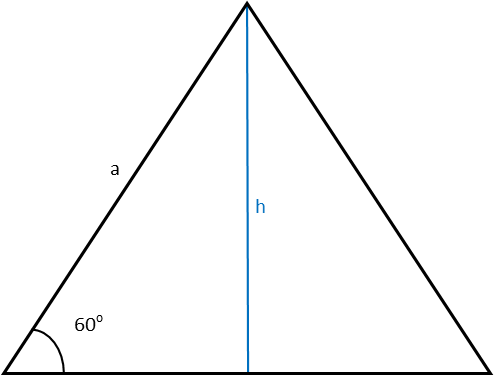
Equilateral triangle

In an equilateral triangle, all three sides have the same length.

This also means that all angles are always equal.

Image of an equilateral triangle

The sum of the angles in a triangle is always 180^o, so it is possible to calculate the angle without knowing anything else about the triangle.

You just need to divide 180 by 3:

$$ \frac{180^\circ}{3}=60^\circ $$

The angles in an equilateral triangle are always 60 degrees.

If you know either the height or the side length, it is possible to calculate the rest of the triangle.

The height divides the triangle into two equal right-angled triangles, so you can use formulas for right-angled triangles.

Calculator

$$ a=\frac{P}{3} $$

$$ a=\frac{h}{sin(60)} $$

$$ a=2\cdot \frac{Area}{h} $$

$$ h = cos(30)\cdot a $$

$$ h=sin(60)\cdot a $$

$$ h = \frac{\sqrt{3}}{2} \cdot a $$

$$ h=\sqrt{a^2- \biggl( \frac{a}{2}\biggr)^2} $$

$$ h= \frac{2\cdot Area}{a} $$

$$ A=\frac{h\cdot a}{2} $$

$$ A=\frac{\sqrt{3}}{4}\cdot a^2 $$

$$ A= \frac{1}{2} \cdot \sqrt{a^4 - \biggl( \frac{a^2}{2}\biggr)^2} $$

$$ P=3\cdot a $$

$$ P= 3\cdot \frac{h}{sin(60)} $$