Square numbers

A Square Number is the result of raising a Number to the second power.

In other words, a Square Number has the form \(\large n^2\), where \(n\) is a Natural Number.

 

Example

\(\large 3^2 = 9,\quad 6^2 = 36,\quad 10^2 = 100\)

 

If you take the Square Root of \(X\) and the result is a Whole Number, then \(X\) is a Square Number. For example, \(\large \sqrt{81} = 9\), so 81 is a Square Number.

 

Geometric meaning

A Square Number can be seen as the area of a Square with side length \(n\). For example, 16 is the area of a Square with side length 4.

 

\(\large \sqrt{16} = 4\)

 

Parabola in the coordinate system

The points \((n, n^2)\) form the graph of the function \(\large y = x^2\), which is a Parabola.

 

 

 

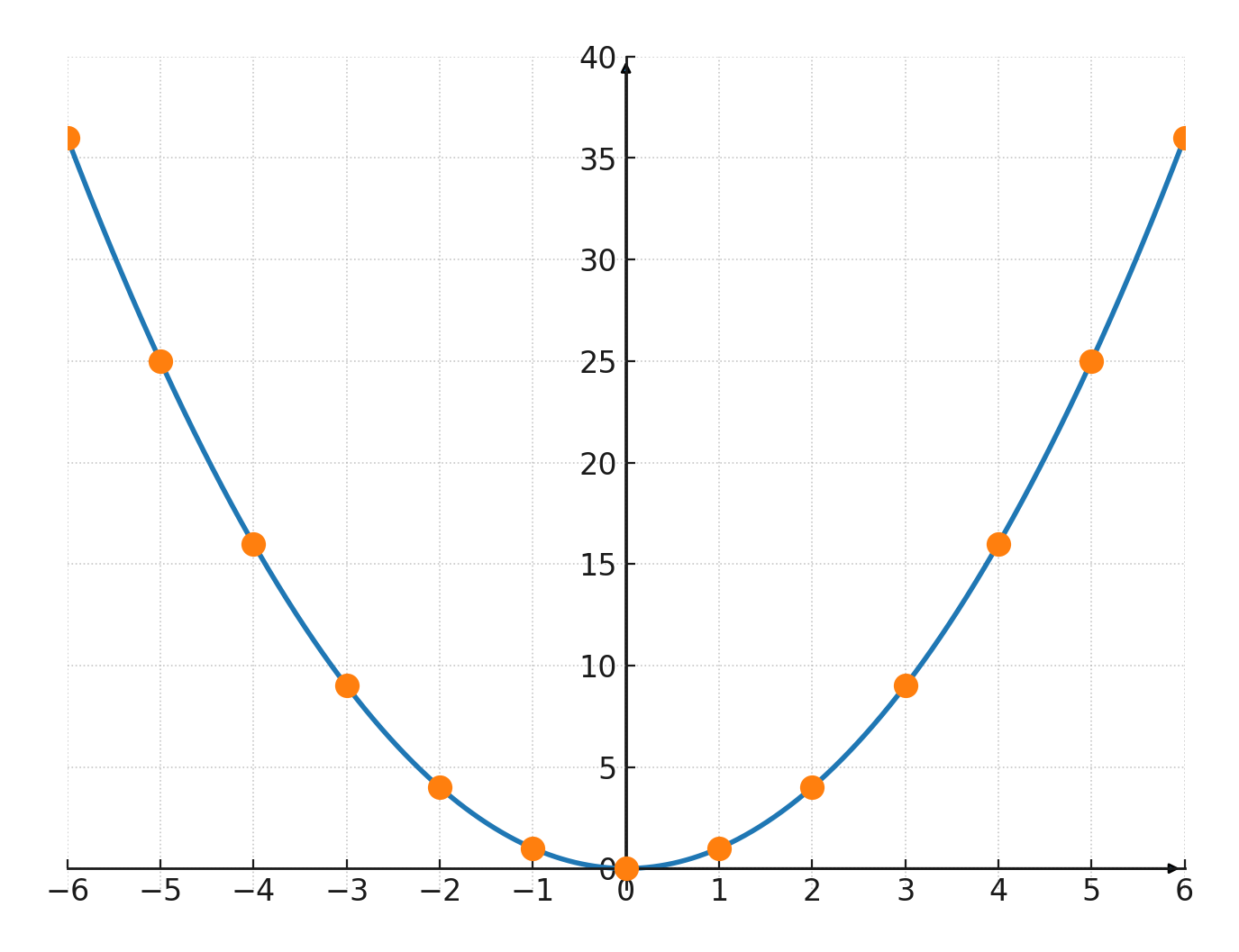
Table of the first Square Numbers

 

Number (root)	1	2	3	4	5	6	7	8	9	10
Square Number	1	4	9	16	25	36	49	64	81	100

 

 

Patterns in Square Numbers

Difference between two consecutive Square Numbers:

 

\(\large (n+1)^2 - n^2 = 2n + 1\). The difference is always an odd Number.

 

Sum of the first \(n\) odd Numbers:

 

\(\large 1 + 3 + 5 + \cdots + (2n-1) = n^2\). For example \(\large 1+3+5+7+9 = 25\).

 

Last digit:

 

A Square Number can only end with 0, 1, 4, 5, 6 or 9.

 

Modulo 3:

 

A Square Number is either divisible by 3 or one more than a multiple of 3. That is \(\large n^2 \equiv 0\) or \(\large 1 \pmod{3}\).

 

 

Square Numbers and Prime Factors

A Number is a Square Number if and only if all exponents in its Prime Factorization are even Numbers.

 

For example \(\large 900 = 2^2 \cdot 3^2 \cdot 5^2 = (2\cdot 3\cdot 5)^2\), so it is a Square Number.

 

 

Connections to other topics

Pythagoras:

 

Square Numbers appear in Pythagoras’ Theorem \(\large a^2 + b^2 = c^2\). A classic example is \(\large 3^2 + 4^2 = 5^2\), that is \(\large 9 + 16 = 25\).

 

Difference of Squares:

 

\(\large a^2 - b^2 = (a-b)(a+b)\) is often used in rewriting and factorization.