Fibonacci numbers

Fibonacci numbers are named after Leonardo Fibonacci, an Italian mathematician, who described this sequence for the first time in the year 1202 in the book Liber Abaci.

 

Recursive definition

The Fibonacci numbers are defined by a recursive function:

 

$$ F_0 = 0, \quad F_1 = 1 $$

$$ F_n = F_{n-1} + F_{n-2} \quad (n \geq 2) $$

 

This means that each number in the sequence is the sum of the two preceding ones.

The first 10 Fibonacci numbers are therefore:

 

$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 $$

 

You can quickly see the pattern:

 

$$ 0+1=1,\;\;1+1=2,\;\;1+2=3,\;\;2+3=5,\;\;3+5=8\;\;etc. $$

 

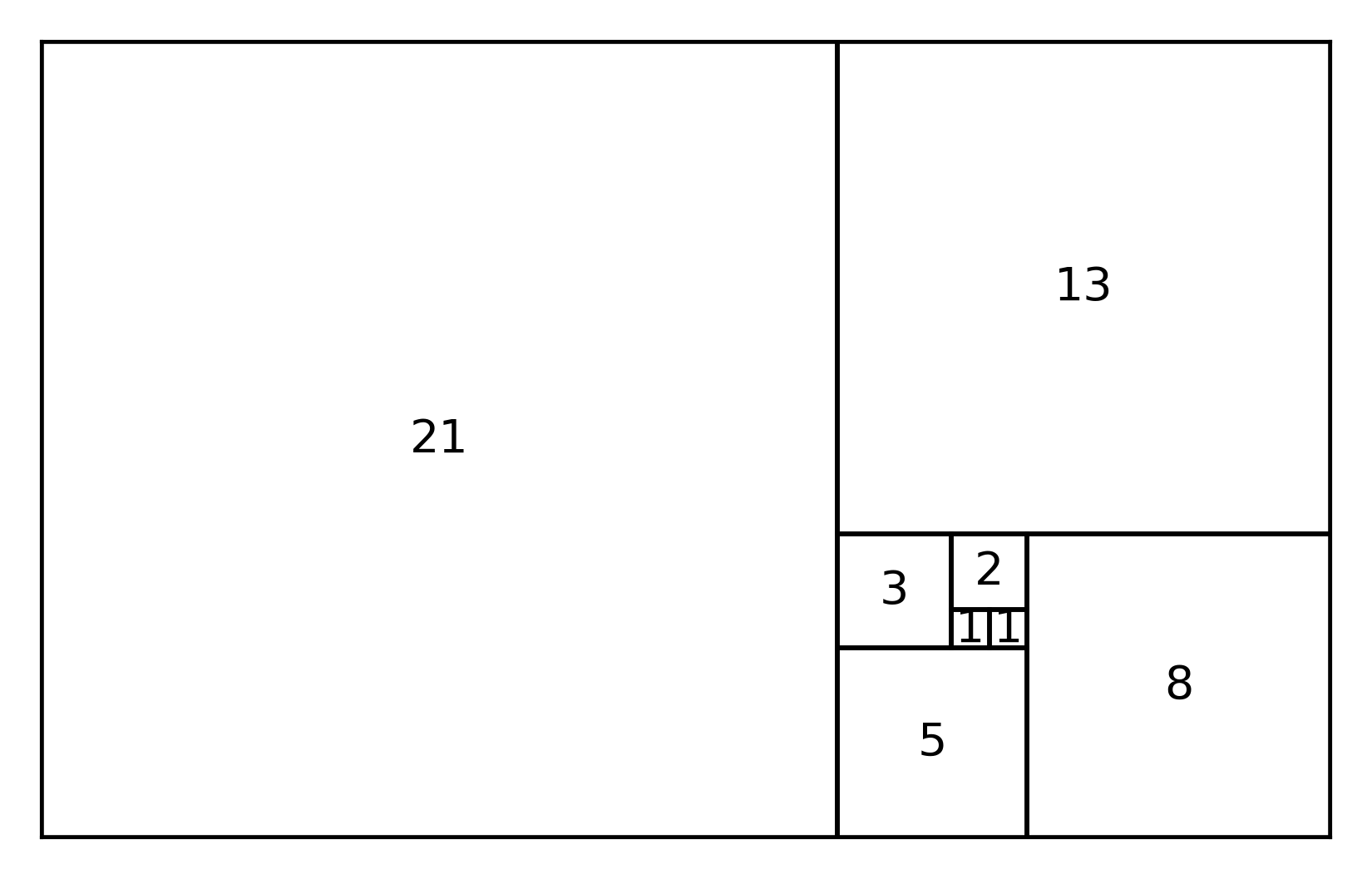
Fibonacci numbers can be illustrated with squares whose side lengths equal the numbers. 

 

 

 

The ratio between Fibonacci numbers

If you take the ratio between two consecutive Fibonacci numbers, the result approaches a constant called the golden ratio \(\phi\):

 

$$ \phi = \frac{1+\sqrt{5}}{2} \approx 1,618... $$

 

Example: $$ \frac{55}{34} \approx 1,6176 $$ The larger the numbers, the closer you get to \(\phi\).

 

 

Binet’s formula

There is an explicit formula (called Binet’s formula) that makes it possible to calculate a Fibonacci number without knowing the previous ones:

 

$$ F_n = \frac{1}{\sqrt{5}}\Biggl(\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n - \Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n\Biggr) $$

 

Using Binet’s formula we can calculate:

 

$$ F_{25} = 75025 $$

 

The 25th Fibonacci number is therefore 75025.

 

 

The Fibonacci spiral

When drawing the Fibonacci squares, a spiral can be drawn from the center outward. This spiral is found in many natural patterns: sunflower seeds, shells, cauliflower.

 

 

There are many places where we see and use the Fibonacci numbers and the spiral in daily life:

 

• Nature – plant growth, flower patterns, seeds and shells.
• Art and architecture – proportions and compositions based on Fibonacci and the golden ratio.
• Computer science – algorithms, data structures (Fibonacci heap) and efficient search.
• Music – some composers have used Fibonacci numbers to structure rhythms and measures.

 

 

Patterns in Fibonacci numbers

The sum of the first \(n\) Fibonacci numbers:

 

The sum is always one less than the \((n+2)\)-th Fibonacci number:

$$ F_1 + F_2 + \cdots + F_n = F_{n+2} - 1 $$

 

Example:

The first 5 Fibonacci numbers are \(1,1,2,3,5\). The sum is:

$$ 1+1+2+3+5 = 12 $$

The 7th Fibonacci number is 13, and \(13-1=12\). The rule holds.

 

The sum of the squares of the Fibonacci numbers:

 

The sum of the squares up to \(F_n\) equals the product of \(F_n\) and \(F_{n+1}\):

$$ F_1^2 + F_2^2 + \cdots + F_n^2 = F_n \cdot F_{n+1} $$

 

Example 1:

For \(n=3\):

$$ 1^2+1^2+2^2+3^2 = 15 $$

And at the same time:

$$ 3 \cdot 5 = 15 $$

 

Example 2:

For \(n=5\):

$$ 1^2+1^2+2^2+3^2+5^2 = 40 $$

And:

$$ 5 \cdot 8 = 40 $$

 

The rule holds for all Fibonacci numbers.

 

Other patterns:

• Every second Fibonacci number is even.
• Every third is divisible by 2, every fourth by 3, etc.
• The Fibonacci numbers can be found as diagonal sums in Pascal’s triangle.

 

 

Summary

The Fibonacci sequence starts simply: \(0, 1, 1, 2, 3, 5...\), but it contains deep patterns and connections to nature, art and mathematics.

From recursive definitions to Binet’s formula and the golden ratio, Fibonacci numbers are both beautiful and practical.