Numbers

Numbers are a broad concept, fundamentally used to indicate a Quantity or a Size.

There are many different Types of Numbers, which are divided into Categories. In Mathematics we work with all of them, and they can be seen as nested Sets, where each new Category extends the previous one.

Below is a short description of the most important Categories.

 

Natural Numbers \(\ N\)

The Natural Numbers are all whole Numbers greater than zero: 1, 2, 3, 4, 5, 6 … etc. They are denoted by \(\large N\). In some contexts, zero is also included, and then one writes \(\large N_0\).

 

Integers \(\ Z\)

If we extend the Natural Numbers (including 0) with the negative Numbers, we get the Integers:

… -4, -3, -2, -1, 0, 1, 2, 3 … etc.

They are denoted by \(\large Z\).

 

Rational Numbers \(\ Q\)

The Rational Numbers are all Numbers that can be written as a Fraction, where the Numerator is an Integer and the Denominator is a Natural Number different from 0. Examples:

 

\(\large \frac{1}{4} = 0.25\), \(\large -\frac{3}{5} = -0.6\)

 

All finite and periodic Decimal Fractions also belong here.

They are denoted by \(\large Q\).

 

Real Numbers \(\ R\)

The Real Numbers include all the previously mentioned Sets of Numbers, but also the Irrational Numbers, which cannot be written as Fractions. Irrational Numbers have an infinite non periodic Decimal expansion.

 

Examples are \(\large \pi\) and \(\large \sqrt{5}\).

 

\(\large \sqrt{5} \) is a Real Number, but at the same time an Irrational Number, because it cannot be written as a Fraction.

The Real Numbers are denoted by \(\large R\).

 

Complex Numbers \(\ C\)

The Complex Numbers extend the Real Numbers by including the Imaginary Numbers. Where a Real Number can be placed on a Number Line, a Complex Number can be represented in the Plane as a Point with the Coordinates \(\large (x,y)\), where \(x\) is the Real Part, and \(\large y\) is the Imaginary Part. A Complex Number is written in the form:

 

\(\large z = x + yi \)

 

Here \(i\) is the Imaginary Unit, defined by \(\large i^2 = -1\). An example is:

 

\(\large z = 3 + 2i \)

 

This can be understood as the Point \(\large (3,2)\) in the Complex Plane.

Complex Numbers are used for example to solve Equations that have no Real Solutions, such as:

 

\(\large x^2 + 1 = 0 \implies x = \pm i \)

 

The Complex Numbers are denoted by \(\large C\).

 

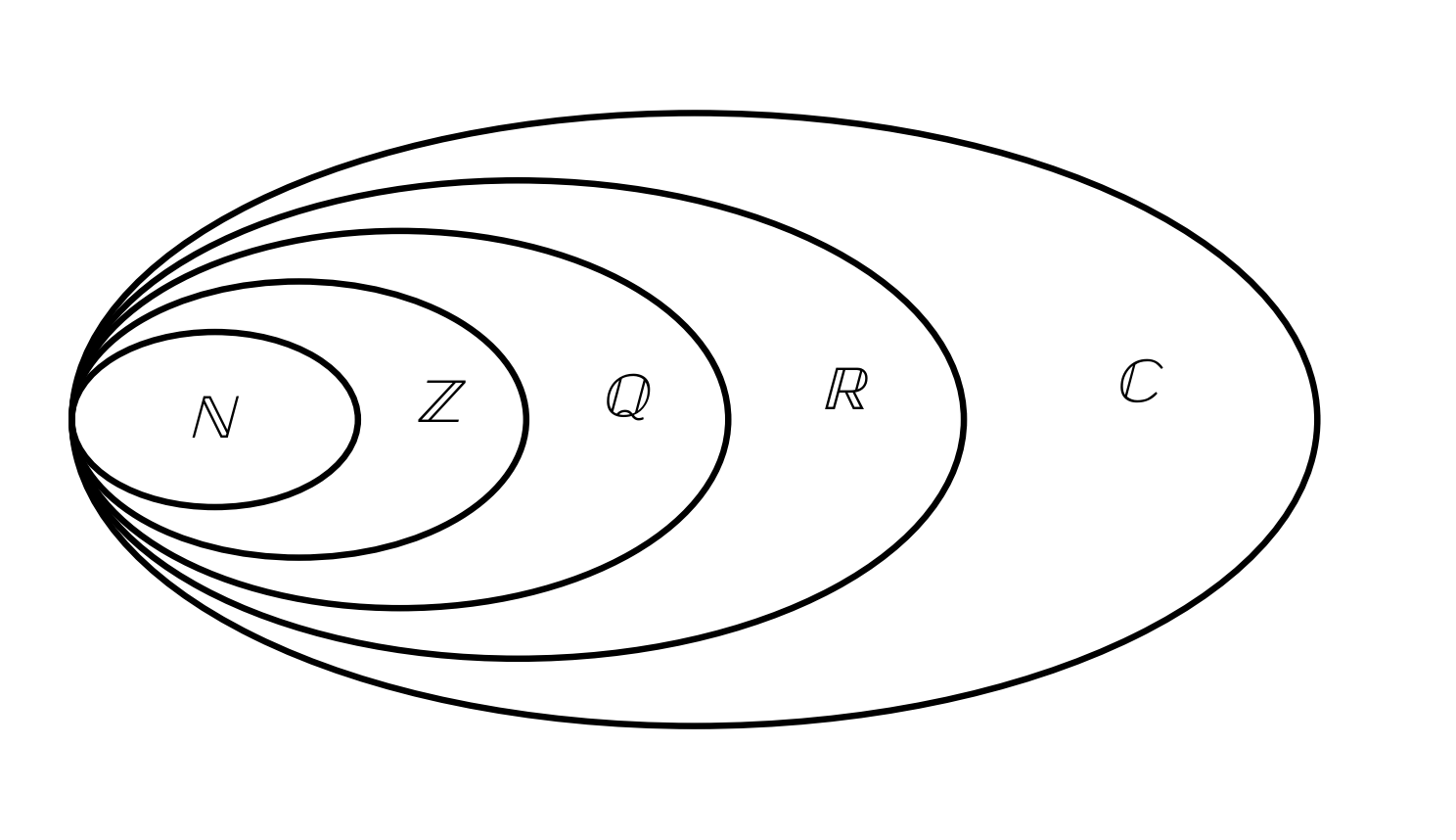
The Picture shows the Natural Numbers as part of the Integers, which are part of the Rational Numbers, etc.

 

Summary

The Hierarchy between the Number Sets can be written briefly as:

 

\(\Large N \subset Z \subset Q \subset R \subset C\)