Rational functions

A rational function is a fraction where both the numerator and denominator are polynomials. Thus, a rational function can be written as:

 

$$ \large f(x) = \frac{P(x)}{Q(x)} $$

 

Here, \(P(x)\) and \(Q(x)\) are polynomials, and the denominator \(Q(x)\) must not be equal to 0.

Rational functions can have vertical asymptotes where the denominator becomes 0, and they can have horizontal or oblique asymptotes, depending on the degree of the numerator and denominator.

 

Example of a rational function

An example of a rational function is:

 

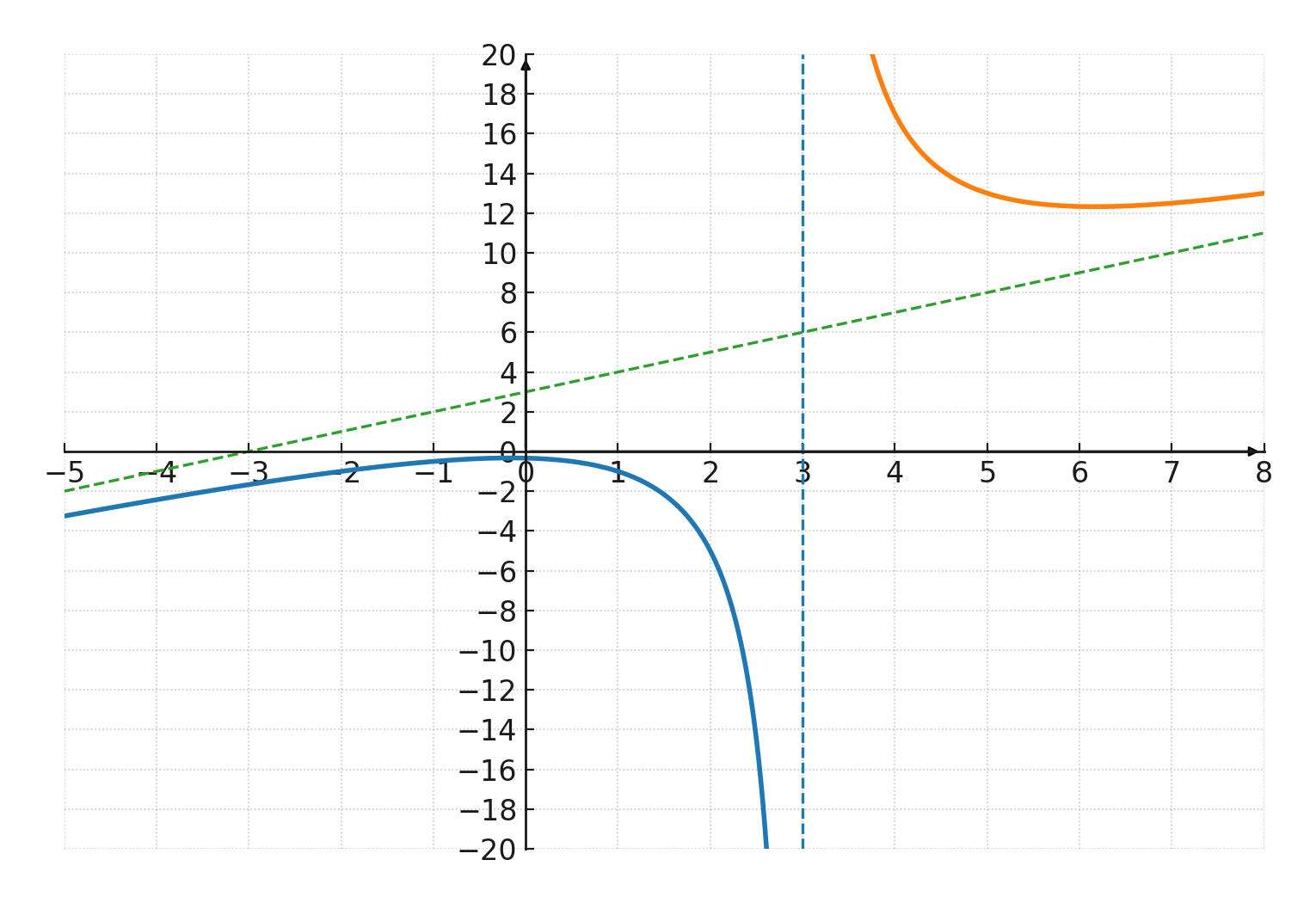
$$ \large f(x) = \frac{x^2+1}{x-3} $$

 

In this example, the numerator is \(x^2+1\), which is a 2nd degree polynomial, and the denominator is \(x-3\), which is a 1st degree polynomial.

 

• The function is not defined for \(x=3\), because division by 0 is not allowed.
• The graph therefore has a vertical asymptote at \(x=3\).
• When \(x\) becomes very large or very small, the fraction behaves approximately like \(\tfrac{x^2}{x} = x\). Therefore, the graph has an oblique asymptote close to the line \(y=x\).

 

 

 

Inverse proportionality

One of the simplest types of rational functions is the inverse proportional function:

 

$$ \large f(x) = \frac{k}{x} $$

 

Here, \(k\) is a constant. The function is not defined for \(x=0\), because division by zero is not possible.

The graph has a characteristic shape, lying in the 1st and 3rd quadrants if \(k\) is positive, and in the 2nd and 4th quadrants if \(k\) is negative.

 

This function is called inverse proportional because when \(x\) becomes twice as large, \(f(x)\) becomes half as large. The product \(x \cdot f(x)\) is always the same (equal to \(k\)).