Inverse proportional function

A function is inversely proportional when the following holds:

$$ y \cdot x=k $$

This means that if you multiply the two coordinates, x and y, together, all coordinate pairs give the same result (k).

For example, the following coordinate pairs:

$$ (1,20) = 1 \cdot 20 = 20 $$

$$ (2,10) = 2 \cdot 10 = 20 $$

$$ (4,5) = 4 \cdot 5 = 20 $$

$$ (5,4) = 5 \cdot 4 = 20 $$

$$ (10,2) = 10 \cdot 2 = 20 $$

$$ (20,1) = 20 \cdot 1 = 20 $$

If you plot these coordinate pairs in a system, you get the curve shown below, which always has asymptotes along both axes.

This means that it can get very close to the axes, but it will never cross them.

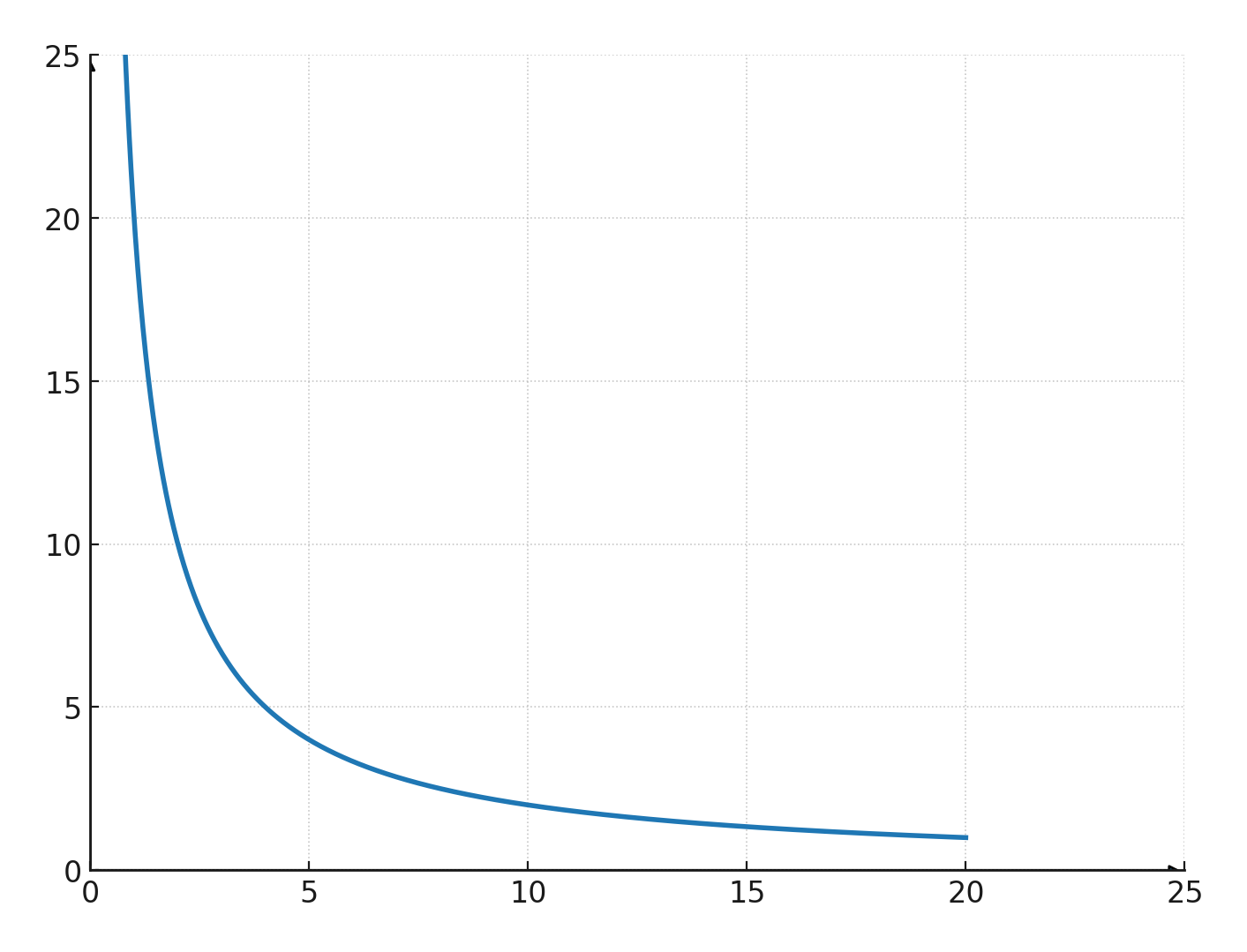
Inverse proportional function - Hyperbola

k is called the proportionality constant.

The function rule for inverse proportionality is written like this:

$$ f_{(x)} = \frac{k}{x} $$

$ x $ cannot be 0. You cannot divide by 0.

If the constant is 15 and x = 5, then y = 3

$$ y = \frac{15}{5} $$

$$ y = 3 $$

In this way, you can calculate several coordinate pairs with the same constant (15).

Note that if you have found the coordinate $(5,3)$, then $(3,5)$ is also valid.

You can also do it with x = -5, then y = -3

$$ y = \frac{15}{-5} $$

$$ y = -3 $$

If you do it with negative numbers, you will be able to draw another curve, which is a reflection of the first one.

These curves are called a Hyperbola.

Below is drawn a hyperbola with the constant 15

Coordinates for the curve in the 1st quadrant are inserted in the value table:

$\Large x $	1	2	3	5	6	10	15
$\Large y $	15	7.5	5	3	2.5	1.5	1

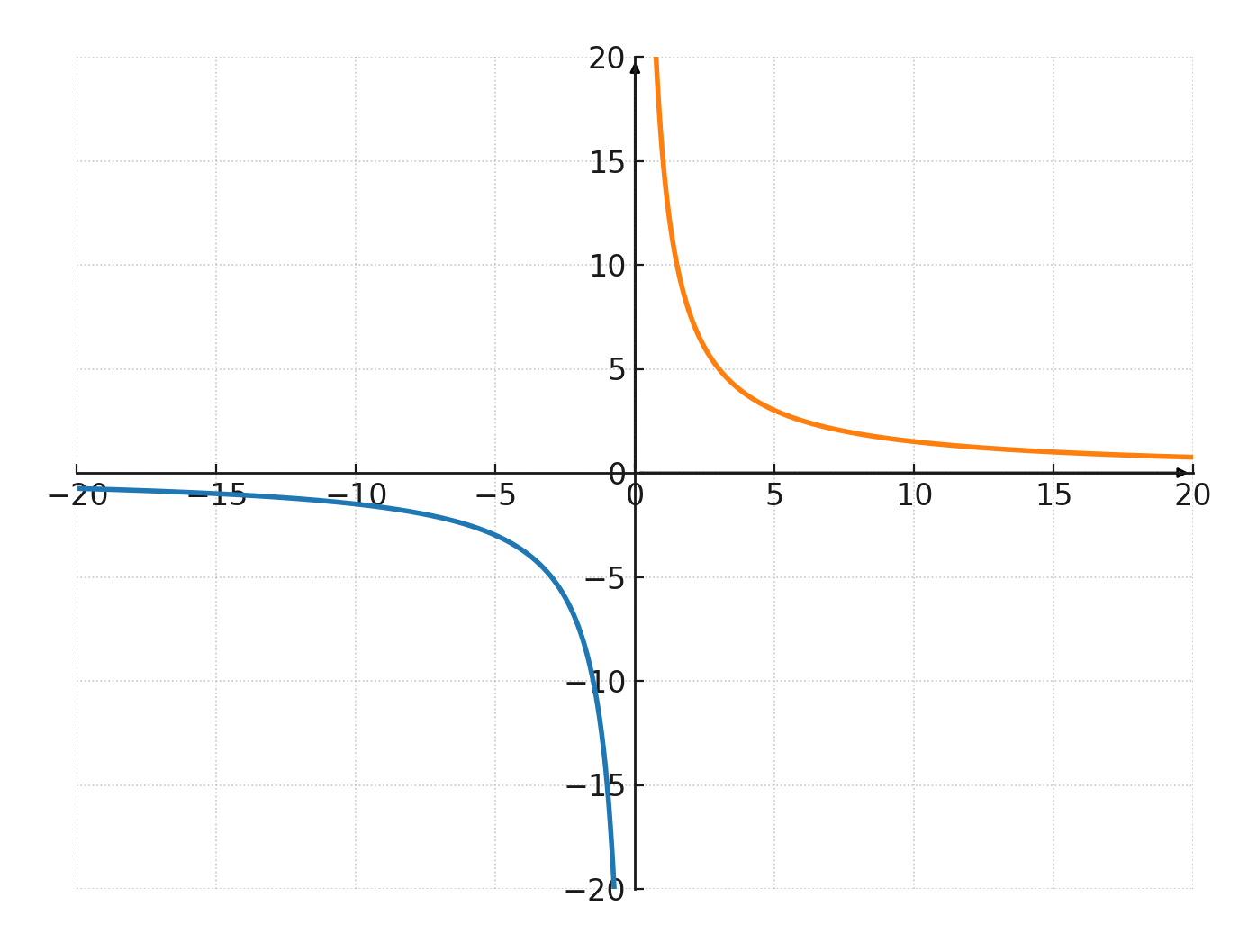
Inverse proportional function - Hyperbola

For the curve in the 3rd quadrant, it also holds that $ x \cdot y = 15$

$\Large x $	-1	-2	-3	-5	-6	-10	-15
$\Large y $	-15	-7.5	-5	-3	-2.5	-1.5	-1

In this example, some coordinates are omitted for space reasons. You should create coordinate pairs for all x from 1-15.

This way, you can draw a more accurate curve.

\(\Large x \)	-1	-2	-3	-5	-6	-10	-15
\(\Large y \)	-15	-7.5	-5	-3	-2.5	-1.5	-1