Asymptotes

An asymptote is a line that the graph of a function gets closer and closer to, without ever intersecting it (or only in isolated points). For rational functions, asymptotes are very common.

 

There are three types of asymptotes:

 

Vertical asymptotes:

Occur where the denominator in a rational function becomes 0. For example, the function \( \Large f(x) = \frac{1}{x-3} \) has a vertical asymptote at \(\large x = 3 \).

The function also has the x-axis as a horizontal asymptote.

 

Horizontal asymptotes:

Occur when the graph of a function approaches a constant value as \(\large x \) becomes very large or very small.

For example, \(\Large f(x) = \frac{2x^2+1}{x^2+3} \) has a horizontal asymptote at \(\large y = 2 \).

 

 

Oblique asymptotes:

Occur when the degree of the numerator is exactly 1 higher than the degree of the denominator.

For example, \(\Large f(x) = \frac{x^2+1}{x+1} \) has an oblique asymptote at the line \(\large y = x - 1 \).

 

 

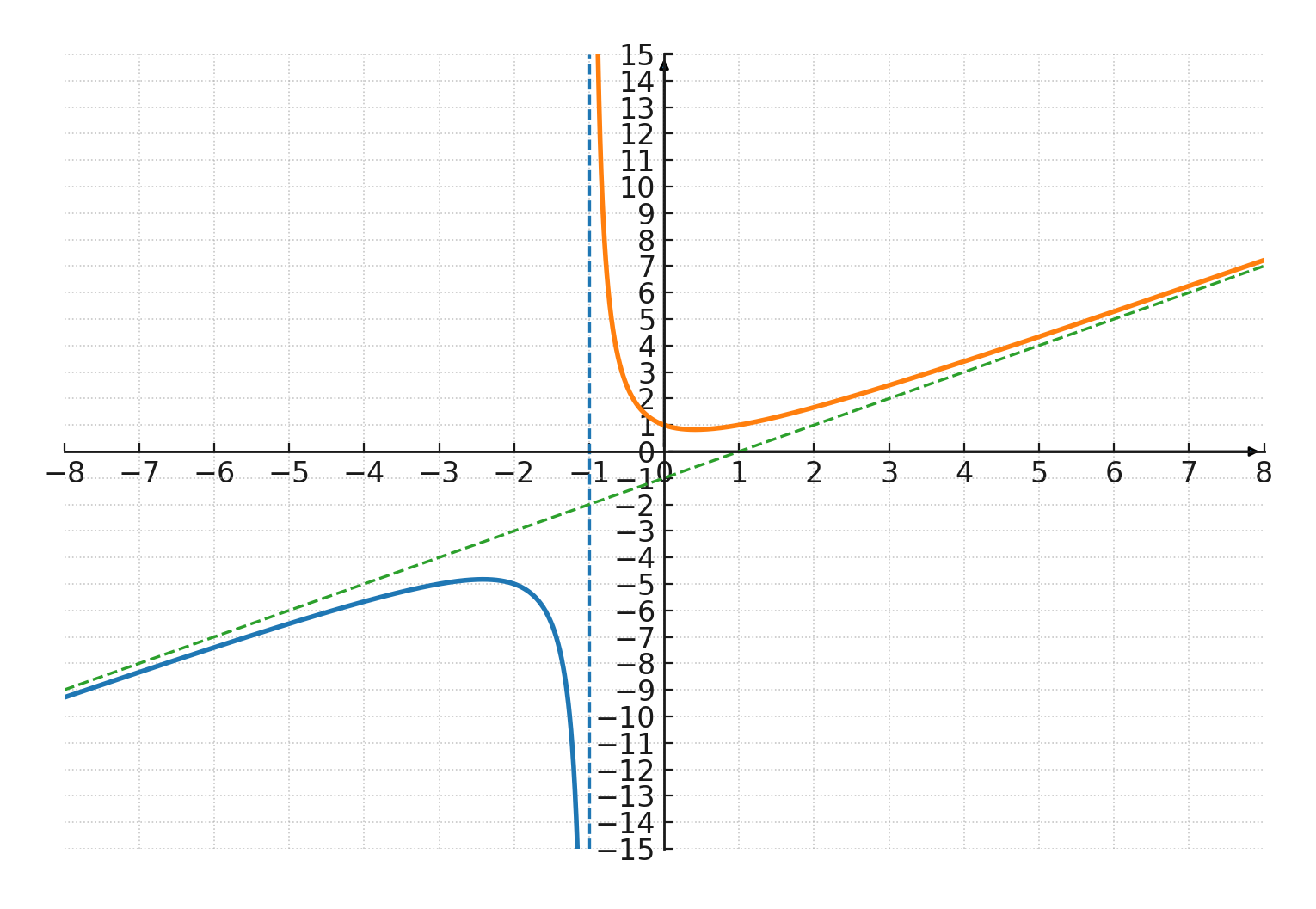
Asymptotes help us understand the behavior of a graph without drawing it completely.