Coordinate system

A coordinate system consists of two number lines that are perpendicular to each other. The number lines are called axes.

The horizontal axis is called the x-axis or the first axis, and the vertical axis is called the y-axis or the second axis.

The two axes intersect at their zero point. This point is called origin.

 

 

Points in the coordinate system

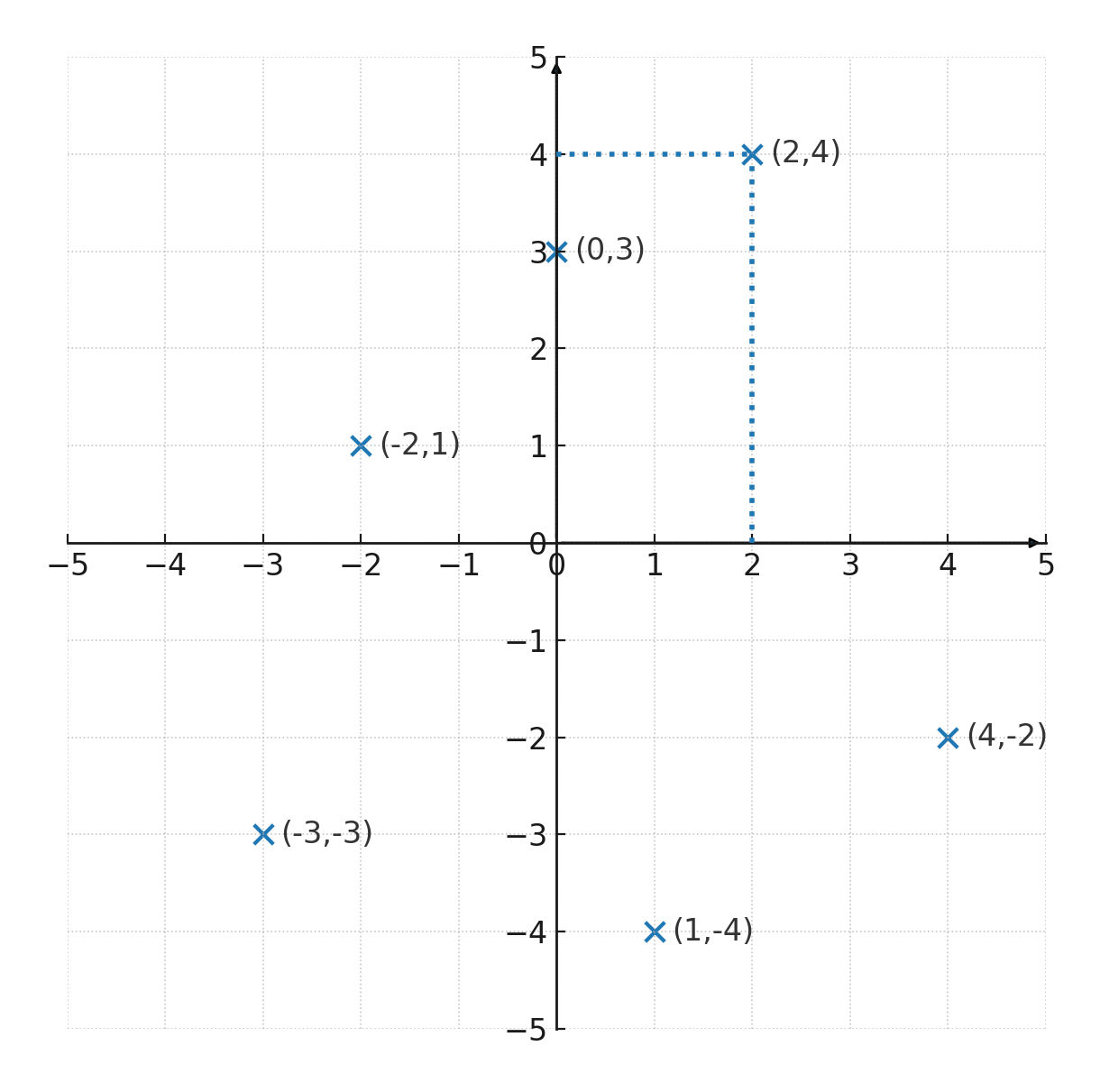
A point in the coordinate system can be read by following a perpendicular line to the axes and reading the value of the x- and y-axis at that point. The x-axis is always read first, so a point is written as \( \large (x,y)\).

In the coordinate system below, different points are marked.

The point \( \large (2,4)\) lies in the coordinate system, where the two perpendicular lines show that:

• x-axis = 2
• y-axis = 4

 

 

 

Quadrants

The four areas in the coordinate system are called quadrants, where:

 

• 1st quadrant: \( \large (x,y)\)
• 2nd quadrant: \( \large (-x,y)\)
• 3rd quadrant: \( \large (-x,-y)\)
• 4th quadrant: \( \large (x,-y)\)

 

Three dimensions

The coordinate system can also be extended to three dimensions by adding a z-axis, which is perpendicular to the x- and y-axes at the origin.

In the two-dimensional system there are four quadrants, but in the three-dimensional system the space is divided into eight areas, called octants.

Points are written with three numbers \( (x,y,z) \). This is used, for example, in solid geometry.