Scalene triangle
A scalene triangle is a triangle where all sides and angles are different, meaning it is neither right-angled, isosceles, nor equilateral.
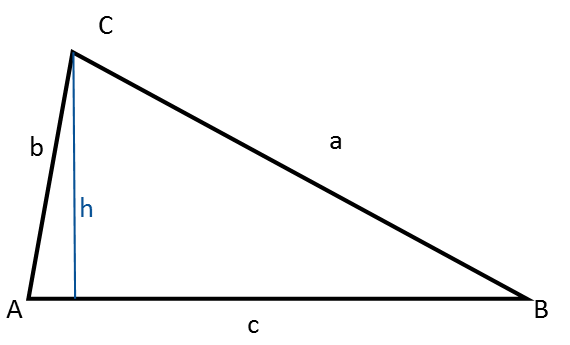
Formulas and methods
To calculate scalene triangles, you need to use the cosine and sine rules.
Be aware that when using the sine rule, ambiguity may arise, in some cases there are two possible triangles that match the given data and thus two solutions.
Read more about the cosine and sine rules under Trigonometry.
To calculate a scalene triangle, you need to know one side length and at least two other pieces of information about the triangle.
In some cases, the height of the triangle can be used instead of a side length in calculations.
Note that the height of the triangle divides it into two right-angled triangles. This can be helpful in some calculations because it makes it possible to use trigonometry for right-angled triangles and the Pythagorean theorem.
But REMEMBER: You must not use formulas for right-angled triangles unless the triangle is actually right-angled!
They can only be used if you divide the triangle into two right-angled triangles and work with those.
On the right, you can find all formulas for calculating scalene triangles.