Isosceles triangle

An isosceles triangle has two equal-length sides (legs) and two equal angles, which lie opposite the two equal-length sides.

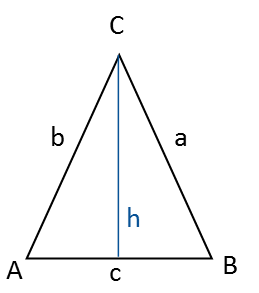
Image of an isosceles triangle

If you know one of the angles and either the height or one of the sides, you can calculate the remaining sides and angles of the triangle.

Tips for calculation

If you know one of the angles, it is always possible to calculate the other two, because the sum of all three angles must be 180 degrees.

If angle C is 70 degrees, then angle A and B will be 55 degrees, because those two angles are equal.

$$ \angle A+\angle B = 180^\circ - 70^\circ = 110^\circ \\[14pt] $$

$$ \angle A=\angle B=\frac{110^\circ}{2}=55^\circ $$

If angle A is 35 degrees, then angle B is also 35 degrees and angle C will be 110 degrees because:

$35+35+110=180$

The height from angle C down to side c (opposite) divides the triangle into two mirrored right-angled triangles. Therefore, you can use Pythagoras’ theorem and trigonometric functions for calculations.

Side c is the base of the triangle, and angle C is its apex.

Calculator

Formulas

Side a

$$ a=b=\frac{h}{sin(A)} $$

$$ a=b=\frac{c}{2\cdot cos(A)} $$

$$ a=b=\frac{h}{cos\biggl(\frac{\angle C}{2} \biggr)} $$

$$ a=b=\frac{c}{2\cdot sin\biggl(\frac{\angle C}{2} \biggr)} $$

$$ a=b=\sqrt{h^2 + \biggl(\frac{c}{2} \biggr)^2} $$

Side c

$$ c=2\cdot \sqrt{a^2-h^2} $$

$$ c=2\cdot b\cdot cos(A) $$

$$ c=2\cdot b\cdot sin\biggl(\frac{\angle C}{2}\biggr) $$

$$ c=2\cdot h\cdot tan\biggl(\frac{\angle C}{2}\biggr) $$

$$ c=2\cdot \frac{h}{tan(A)} $$

Height

$$ h=b\cdot sin(A) $$

$$ h=\frac{c}{2}\cdot tan(A) $$

$$ h=\frac{c}{tan(C)} $$

$$ h=b\cdot cos\biggl(\frac{\angle C}{2} \biggr) $$

$$ h=\sqrt {b^2-\biggl(\frac{c}{2}\biggr)^2} $$

Angle A

$$ A=B=\frac{180-C}{2} $$

$$ A=B=tan^{-1}\biggl(\frac{2\cdot h}{c}\biggr) $$

$$ A=B=sin^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ A=B=cos^{-1}\biggl(\frac{c}{2\cdot a}\biggr) $$

Angle C

$$ C=2\cdot cos^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ C=2\cdot sin^{-1}\biggl(\frac{c}{2\cdot a}\biggr) $$

$$ C=2\cdot tan^{-1}\biggl(\frac{c}{2\cdot h}\biggr) $$

Area

$$ A= \frac{h\cdot c}{2} $$

$$ A= \frac{a\cdot b\cdot sin(C)}{2} $$

$$ A= \frac{a\cdot c\cdot sin(B)}{2} $$

$$ A= \frac{b\cdot c\cdot sin(A)}{2} $$

$$ A= \frac{1}{2} \cdot \sqrt{a^2\cdot c^2 - \biggl( \frac{a^2+c^2-b^2}{2}\biggr)^2} $$

Perimeter

$$ P=a+b+c $$

$$ P=\frac{h}{sin(A)}+\frac{h}{sin(B)}+\frac{h}{tan(A)}+\frac{h}{tan(B)} $$