Triangles
The first polygon.
In plane geometry, the triangle is the first polygon. It is the figure with the fewest sides.
The basic elements of the triangle
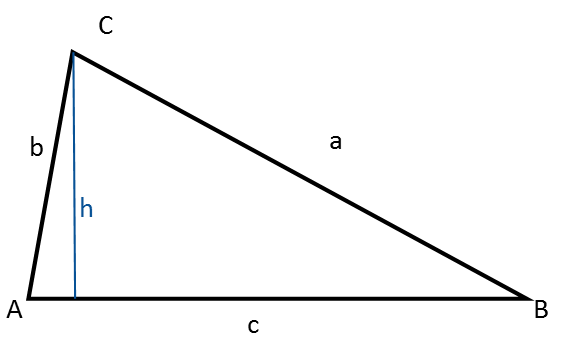
A triangle has:
- Three angles, always denoted by capital letters: A, B, C
- Three sides, always denoted by lowercase letters: a, b, c
- An angle sum of 180°
The height in a triangle
The height in a triangle is a line that goes perpendicular from a vertex down to the opposite side (the base).
A triangle has three heights, one for each side, depending on which is chosen as the base.
Types of triangles
Not all triangles are the same, which is why some are also easier to calculate than others.
Triangles are divided into different types, depending on their sides and angles.
By angles:
- If one of the angles is 90°, we call it a Right-Angled Triangle
- If one of the angles is greater than 90°, we call it an Obtuse Triangle
- If all angles are less than 90°, we call it an Acute Triangle
By sides:
- If two of the sides are the same length, we call it an Isosceles Triangle
- If all three sides are the same length, we call it an Equilateral Triangle
The triangle you see in the figure above is called a Scalene Triangle.
- It has no angles of 90°
- It has no sides that are the same length.
- All angles are under 90°, so it is also an Acute Triangle
A triangle can in fact have several properties. For example, it can be both Right-Angled and Isosceles.
Calculating triangles
Humans have been calculating triangles for thousands of years.
The ancient Greeks already worked with geometry long before our era.
One of the most famous was Pythagoras, who formulated the Pythagorean Theorem, a method for calculating the sides of a right-angled triangle.
Later came trigonometry, a branch of mathematics that allows the calculation of angles and sides in all types of triangles.
Trigonometry was originally developed by Greek astronomers but has since been further developed by mathematicians around the world and is used today in everything from architecture to space exploration.