Das rechtwinklige Dreieck hat, wie der Name schon andeutet, immer einen rechten Winkel.

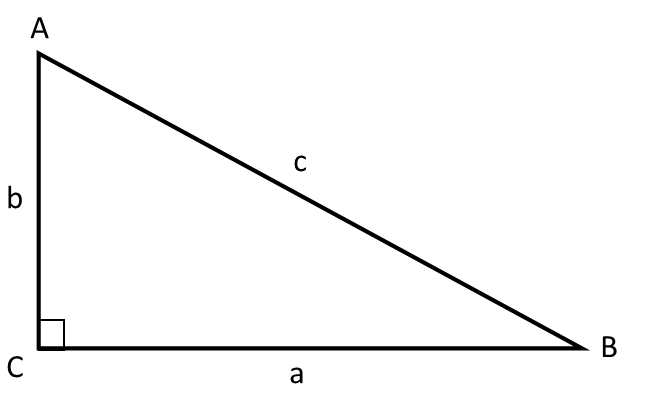
Der rechte Winkel heißt Winkel C.

Die Winkel in Dreiecken werden immer mit Großbuchstaben und die Seiten mit Kleinbuchstaben bezeichnet.

Seite a und Seite b werden Katheten genannt und bilden den rechten Winkel.

Seite c heißt Hypotenuse und ist immer die längste Seite im Dreieck. 

Beachte, dass Seite a gegenüber Winkel A liegt. 

Dasselbe gilt für Seite b und Seite c, und so wird es immer sein.

Pythagoras-Lehrsatz

Der Pythagoräische Lehrsatz beschreibt das Verhältnis der Seiten in einem rechtwinkligen Dreieck.

Pythagoras sagt, dass "das Quadrat der Seite a + das Quadrat der Seite b = das Quadrat der Seite c" gilt.

$$ a^2+b^2=c^2 $$

Wenn wir ein Dreieck haben, in dem \(a=3\) und \(b=4\) ist, erhalten wir Folgendes:

$$ \begin{align} 3^2 + 4^2 &= c^2 \Leftrightarrow \\ 9 + 16 &= 25 \Leftrightarrow \\ c^2 &= 25 \Leftrightarrow \\ c &= \sqrt{25} = 5 \end{align} $$

Aus dem Lehrsatz lassen sich zwei Formeln ableiten, um die Seiten a und b zu berechnen:

$$ a = \sqrt{c^2-b^2} $$

$$ b = \sqrt{c^2-a^2} $$

Abbildung

Die Abbildung zeigt die Quadrate auf den Seiten des Dreiecks.

Du kannst im Abschnitt Trigonometrie nachlesen, wie man Winkel berechnet.

Trigonometrie und rechtwinklige Dreiecke

Im Abschnitt Trigonometrie kannst du über Cosinus, Sinus und Tangens lesen.

Cosinus, Sinus und Tangens können verwendet werden, um Winkel und Seiten in rechtwinkligen Dreiecken zu berechnen.

DENKE DARAN, dass du diese Formeln nicht für Dreiecke verwenden darfst, die nicht rechtwinklig sind.

Für andere Dreiecke musst du die Cosinus- und Sinusgesetze verwenden.

Wenn wir über die Seiten des Dreiecks sprechen, sprechen wir über die "Ankathete" und die "Gegenkathete".

Wenn du dir die Zeichnung ansiehst, kannst du sehen, dass Seite b an Winkel A anliegt, also die Ankathete ist.

Seite a liegt hingegen auf der gegenüberliegenden Seite des Winkel A, daher ist sie die Gegenkathete.

Formeln

In rechtwinkligen Dreiecken verhält es sich folgendermaßen:

$$ \cos(v) = \mathit{Ankathete \over Hypotenuse}$$

$$ \sin(v) = \mathit{Gegenkathete \over Hypotenuse}$$

$$ \tan(v) = \mathit{Gegenkathete \over Ankathete}$$

Durch die Verwendung inverser trigonometrischer Funktionen (arcsin, arccos, arctan) kann man den Winkel direkt berechnen:

$$ v = \cos^{-1}\biggl(\mathit{Ankathete \over Hypotenuse}\biggr)$$

$$ v = \sin^{-1}\biggl(\mathit{Gegenkathete \over Hypotenuse}\biggr)$$

$$ v = \tan^{-1}\biggl(\mathit{Gegenkathete \over Ankathete}\biggr)$$