Gleichschenkliges Dreieck

Ein gleichschenkliges Dreieck hat zwei gleich lange Seiten (Schenkel) und zwei gleiche Winkel, die den beiden gleich langen Seiten gegenüberliegen.

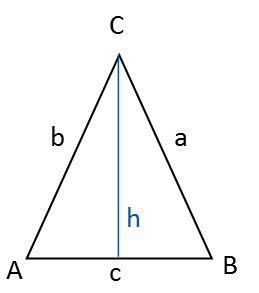
Bild eines gleichschenkligen Dreiecks

Wenn du einen der Winkel und entweder die Höhe oder eine der Seiten kennst, kannst du die übrigen Seiten und Winkel des Dreiecks berechnen.

Tipps zur Berechnung

Wenn du einen der Winkel kennst, kannst du immer die anderen beiden berechnen, da die Winkelsumme in einem Dreieck immer 180 Grad beträgt.

Wenn Winkel C 70 Grad beträgt, sind die Winkel A und B jeweils 55 Grad, da diese beiden Winkel gleich sind.

$$ \angle A+\angle B = 180^\circ - 70^\circ = 110^\circ \\[14pt] $$

$$ \angle A=\angle B=\frac{110^\circ}{2}=55^\circ $$

Wenn Winkel A 35 Grad beträgt, ist Winkel B ebenfalls 35 Grad und Winkel C beträgt 110 Grad, weil:

$35+35+110=180$

Die Höhe von Winkel C zur Seite c (gegenüberliegend) teilt das Dreieck in zwei spiegelbildliche rechtwinklige Dreiecke. Deshalb kannst du den Satz des Pythagoras und trigonometrische Funktionen zur Berechnung verwenden.

Seite c ist die Basis des Dreiecks und Winkel C ist seine Spitze.

Rechner

Formeln

Seite a

$$ a=b=\frac{h}{sin(A)} $$

$$ a=b=\frac{c}{2\cdot cos(A)} $$

$$ a=b=\frac{h}{cos\biggl(\frac{\angle C}{2} \biggr)} $$

$$ a=b=\frac{c}{2\cdot sin\biggl(\frac{\angle C}{2} \biggr)} $$

$$ a=b=\sqrt{h^2 + \biggl(\frac{c}{2} \biggr)^2} $$

Seite c

$$ c=2\cdot \sqrt{a^2-h^2} $$

$$ c=2\cdot b\cdot cos(A) $$

$$ c=2\cdot b\cdot sin\biggl(\frac{\angle C}{2}\biggr) $$

$$ c=2\cdot h\cdot tan\biggl(\frac{\angle C}{2}\biggr) $$

$$ c=2\cdot \frac{h}{tan(A)} $$

Höhe

$$ h=b\cdot sin(A) $$

$$ h=\frac{c}{2}\cdot tan(A) $$

$$ h=\frac{c}{tan(C)} $$

$$ h=b\cdot cos\biggl(\frac{\angle C}{2} \biggr) $$

$$ h=\sqrt {b^2-\biggl(\frac{c}{2}\biggr)^2} $$

Winkel A

$$ A=B=\frac{180-C}{2} $$

$$ A=B=tan^{-1}\biggl(\frac{2\cdot h}{c}\biggr) $$

$$ A=B=sin^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ A=B=cos^{-1}\biggl(\frac{c}{2\cdot a}\biggr) $$

Winkel C

$$ C=2\cdot cos^{-1}\biggl(\frac{h}{a}\biggr) $$

$$ C=2\cdot sin^{-1}\biggl(\frac{c}{2\cdot a}\biggr) $$

$$ C=2\cdot tan^{-1}\biggl(\frac{c}{2\cdot h}\biggr) $$

Fläche

$$ A= \frac{h\cdot c}{2} $$

$$ A= \frac{a\cdot b\cdot sin(C)}{2} $$

$$ A= \frac{a\cdot c\cdot sin(B)}{2} $$

$$ A= \frac{b\cdot c\cdot sin(A)}{2} $$

$$ A= \frac{1}{2} \cdot \sqrt{a^2\cdot c^2 - \biggl( \frac{a^2+c^2-b^2}{2}\biggr)^2} $$

Umfang

$$ P=a+b+c $$

$$ P=\frac{h}{sin(A)}+\frac{h}{sin(B)}+\frac{h}{tan(A)}+\frac{h}{tan(B)} $$