Potenzfunktion

Eine Potenzfunktion ist eine Funktion, bei der die Variable $\large x$ als Basis mit einem festen Exponenten erscheint.

Sie wird in dieser Form geschrieben:

$$ \large f(x)=k \cdot x^a $$

Es gibt einige Bedingungen für $\large k$ und $\large a$:

$\large k \neq 0$
- Wenn $\large k = 0$, ergibt die Funktion immer 0, weil mit 0 multipliziert wird
$\large a$ kann eine ganze Zahl, ein Bruch oder eine negative Zahl sein
- Wenn $\large a$ eine positive ganze Zahl ist, erhält man eine wachsende Polynomkurve
- Wenn $\large a$ ein Bruch ist, erhält man eine Wurzelfunktion
- Wenn $\large a$ negativ ist, erhält man eine fallende Kurve, ähnlich einer umgekehrt proportionalen Funktion

Wenn man eine Potenzfunktion als Graph zeichnet, kann sie je nach Exponent $\large a$ sehr unterschiedliche Formen haben.

$\large a$ bestimmt die Form und Symmetrie der Kurve
$\large k$ bestimmt, wie steil die Kurve ist und ob sie nach oben oder unten zeigt

Der Graph kann die y-Achse im Ursprung schneiden, sofern keine Konstante hinzugefügt wird.

$\large a$ wird Exponent genannt:

Wenn $\large a$ gerade ist, sieht die Kurve wie eine Parabel aus und liegt immer auf derselben Seite der x-Achse
Wenn $\large a$ ungerade ist, geht die Kurve durch den Ursprung und hat unterschiedliche Vorzeichen in den beiden Ästen

$\large k$ zeigt, wie steil die Kurve steigt oder fällt

Betrachten wir diese Funktion:

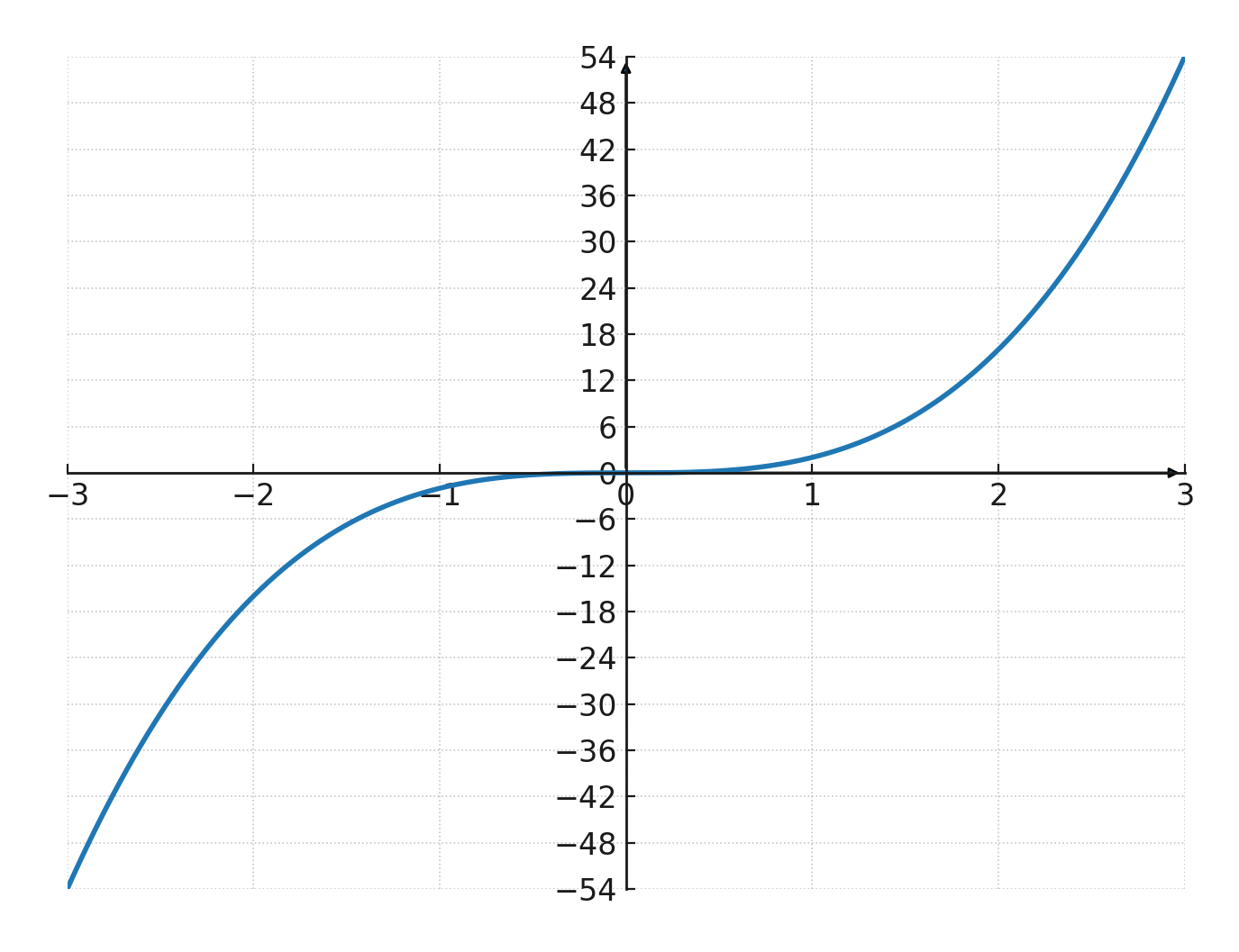
$$ \large y=2 \cdot x^3 $$

Wir sehen, dass es sich um eine Potenzfunktion mit $\large a=3$ handelt, was bedeutet, dass der Graph durch den Ursprung geht und ungerade ist.

Wir sehen auch, dass sie schnell wächst, weil $\large k=2$ sie steiler macht als die Standardfunktion $x^3$.

Wir probieren die Funktion $\large y=2 \cdot x^3$

$\Large x$	-1	-2	-3	1	2	3
$\Large y$	-2	-16	-54	2	16	54

Potenzfunktion

\(\Large x\)	-1	-2	-3	1	2	3
\(\Large y\)	-2	-16	-54	2	16	54