Logarithmusfunktion

Eine Logarithmusfunktion ist die Umkehrung einer Exponentialfunktion. Sie beschreibt die Zahl, auf die eine gegebene Basis potenziert werden muss, um \(\large x\) zu erhalten.

Sie wird in dieser Form geschrieben:

 

$$ \Large f(x)=\log_a(x) $$

 

Es gibt einige Bedingungen für \(\large a\) und für \(\large x\):

 

• \(\large a>0\) und \(\large a \neq 1\)
  • Die Basis darf nicht 1 sein, sonst gibt der Logarithmus keine Variation
• \(\large x>0\)
  • Der Logarithmus ist nur für positive \(\large x\)-Werte definiert

 

Wenn man eine Logarithmusfunktion zeichnet, erhält man eine Kurve, die je nach Basis langsam steigt oder fällt.

• Wenn \(\large a>1\), ist die Funktion wachsend
• Wenn \(\large 0

 

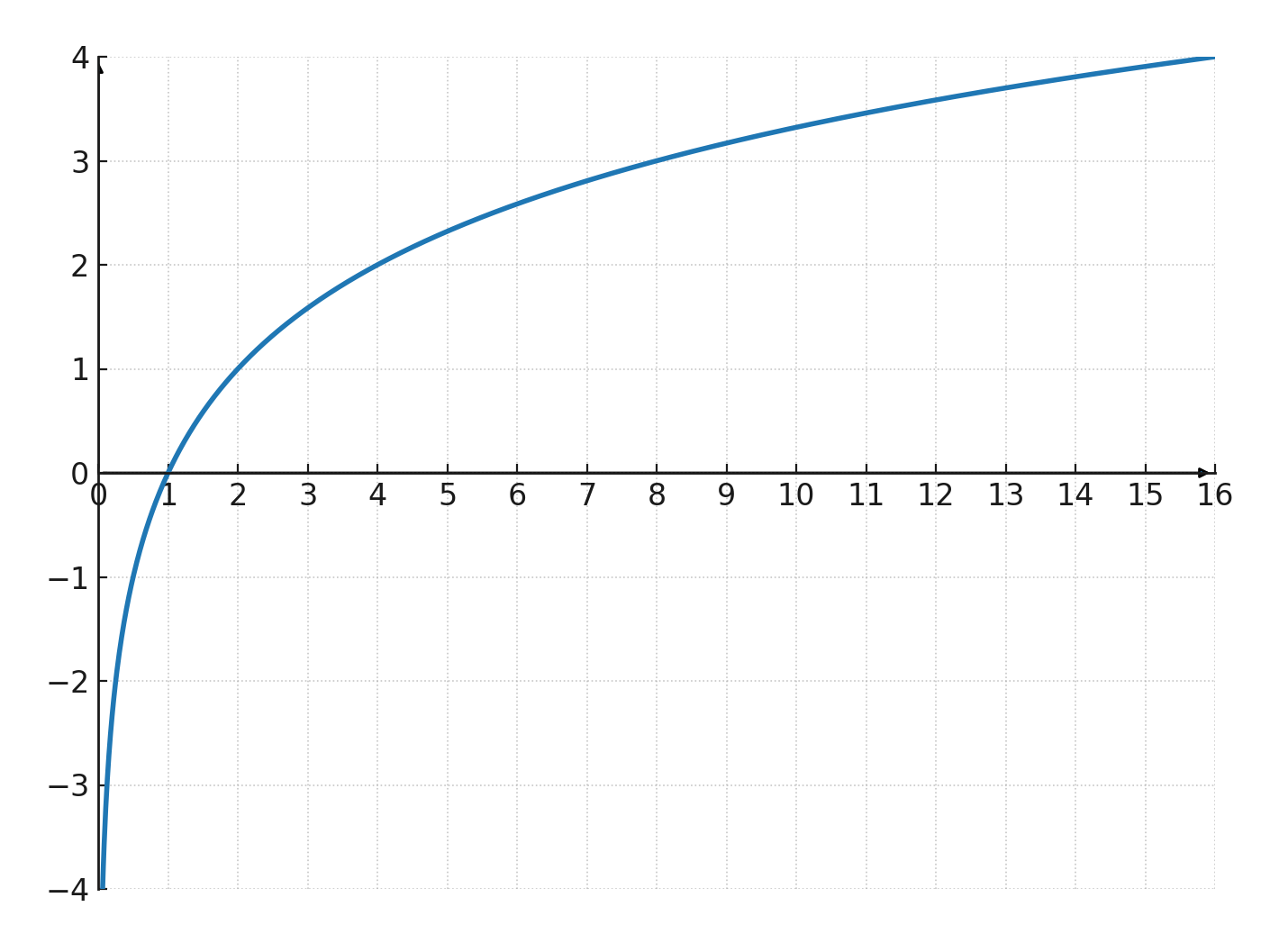
Der Graph hat eine vertikale Asymptote bei \(\large x=0\). Er schneidet die x-Achse bei \(\large (1,0)\). Er schneidet die y-Achse nicht, da die Funktion für \(\large x\le 0\) nicht definiert ist.

 

Basis und Eigenschaften

\(\large a\) wird Basis genannt:

 

• Die Basis bestimmt, ob die Kurve wachsend oder fallend ist
• Eine Änderung der Basis streckt oder staucht die Kurve horizontal

 

Der Logarithmus erfüllt auch die Basiswechsel- und Produktregeln, aber hier konzentrieren wir uns auf die Form des Graphen.

 

Betrachten wir diese Funktion:

 

$$ \Large y=\log_2(x) $$

 

Die Kurve ist wachsend, weil \(\large a=2\) größer als 1 ist. Sie geht durch \(\large (1,0)\) und hat eine vertikale Asymptote bei \(\large x=0\).

 

Beispiel

Wir probieren die Funktion \(\large y=\log_2(x)\)

 

\(\Large x\)	0.25	0.5	1	2	4
\(\Large y\)	-2	-1	0	1	2