Lineare Funktion

Eine lineare Funktion wird in dieser Form geschrieben:

$$ \large f(x)=a \cdot x + b $$

Wenn eine lineare Funktion als Grafik gezeichnet wird, ist sie immer eine gerade Linie.

Die Grafik kann steigend, fallend oder waagerecht sein, je nach $ \large a$, und $ \large b$ gibt an, wo sie die y Achse schneidet

$ \large a$ wird die Steigung genannt:

Wenn $ \large a > 0$ ist die Linie steigend von links nach rechts
Wenn $ \large a < 0$ ist die Linie fallend von links nach rechts
Wenn $ \large a = 0$ ist die Linie waagerecht, weil egal welches $\large x$ ist, $\large y$ bleibt immer gleich.

$ \large b$ gibt an, dass die Linie die y Achse im Punkt $(0,b)$ schneidet

Wenn wir diese Funktion betrachten:

$$ \large y=2x+5 $$

Dann sehen wir, dass es eine steigende Linie ist, weil $\large a=2$.

Wir sehen auch, dass sie die y Achse bei $(0,5)$ schneidet, weil $\large b=5$.

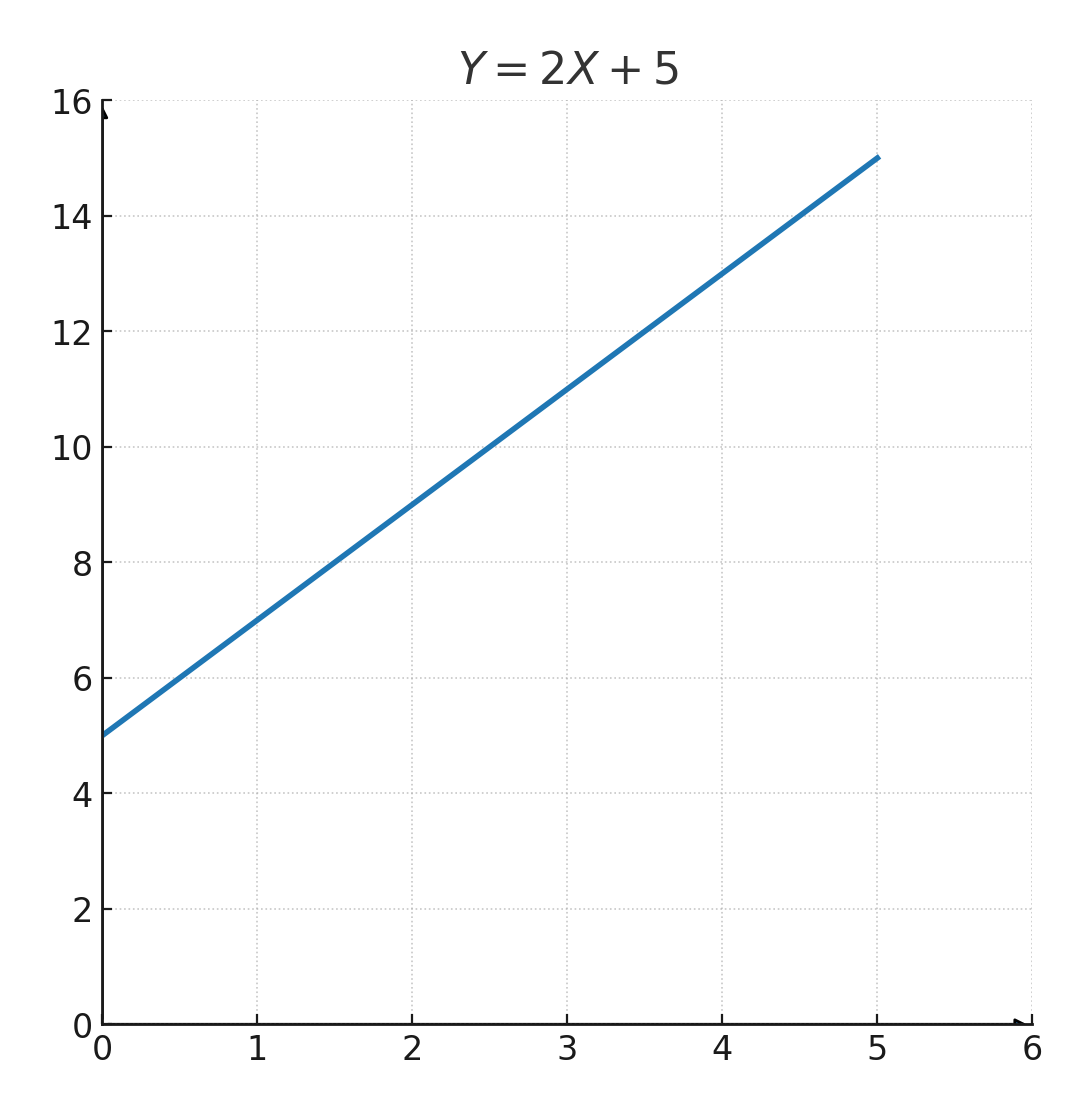
Wir probieren die Funktion: $ \large y=2x+5 $

Die Koordinaten werden in die Wertetabelle unten eingetragen und dann in das Koordinatensystem, sodass die Grafik gezeichnet werden kann:

$\large x$	1	2	3	4	5
$\large y$	7	9	11	13	15

Lineare Funktion

Wenn wir die Koordinaten $(2,9)$ und $(4,13)$ haben, ist es möglich $\large a$ und $\large b$ auf folgende Weise zu finden:

$$ \large a = \frac{y_2-y_1}{x_2-x_1} \Leftrightarrow $$

$$ \large a = \frac{13-9}{4-2} \Leftrightarrow $$

$$ \large a = \frac{4}{2} \Leftrightarrow $$

$$ \large a = 2 $$

Wenn wir $\large a$ gefunden haben, können wir auch $\large b$ mit einer dieser beiden Formeln finden. (Es ist egal welche man benutzt)

$$ \large b = y_1 - a \cdot x_1 $$

$$ \large b = y_2 - a \cdot x_2 $$

Wir benutzen die erste:

$$ \large b = 9 - 2 \cdot 2 \Leftrightarrow $$

$$ \large b = 9 - 4 \Leftrightarrow $$

$$ \large b = 5 $$

Die Funktionsgleichung für die Koordinaten $(2,9)$ und $(4,13)$ ist also:

$$ \large y = ax + b $$

$$ \large y = 2x + 5 $$

\(\large x\)	1	2	3	4	5
\(\large y\)	7	9	11	13	15