Funciones

Una función se usa para describir una relación entre cosas. Si una cosa cambia, entonces otra también cambia.

 

Si sacas un helado del congelador y lo dejas, se derretirá lentamente a medida que pasa el tiempo, porque se calienta.
Por lo tanto, hay una relación entre el tiempo que pasa y la temperatura que sube.

 

También podría ser el precio del helado. Si compras un helado, cuesta 5 euro. Si compras dos helados, cuestan 10 euro, y así sucesivamente.

Una función que puede calcular el precio del helado se ve así:

 

$$ \large y=5x $$

 

Donde \(\large x\) es el número de helados, y \(\large y \) es el precio.

 

La función es un polinomio de primer grado (función lineal).

También es una función proporcional, porque siempre pasará por el origen (el punto \( (0,0) \)).

 

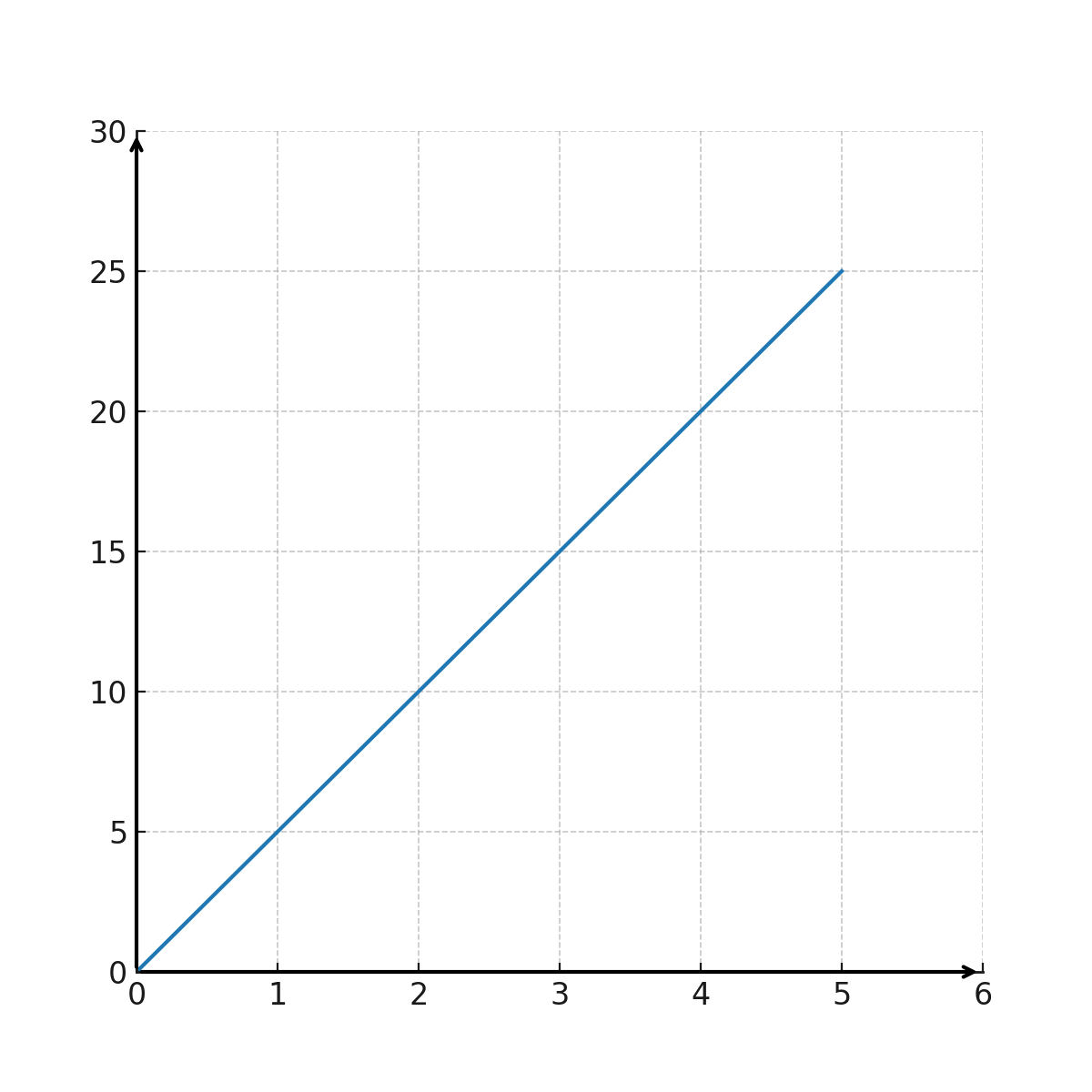
La gráfica muestra la evolución del precio del helado

Número de helados en el eje X y el precio en el eje Y

 

Dibujar una gráfica

Al dibujar la función como una gráfica en un sistema de coordenadas, \(\large x\) se llama variable independiente (número de helados), y \(\large y\) la variable dependiente (el precio).

Cada vez que insertas un valor de \(\large x\) en tu función, puedes calcular el valor correspondiente de \(\large y\) y así ubicar un punto en el sistema de coordenadas.

 

Ejemplo:

• Si insertas \(\large x=1 \) helado en la función, obtienes \(\large y=5 \).

• Si insertas \(\large x=5 \) helados en la función, obtienes \(\large y=25\).

 

Ahora tenemos dos conjuntos de coordenadas \(\large (1,5)\) y \(\large (5,25)\). Cuando se representan en el sistema de coordenadas y se conectan con una línea recta a través del origen, obtenemos la gráfica anterior.