Función lineal
Una función lineal se escribe de esta forma:
$$ \large f(x)=a \cdot x + b $$
Si una función lineal se dibuja como una gráfica, siempre será una línea recta.
La gráfica puede ser creciente, decreciente o horizontal dependiendo de \( \large a\), y \( \large b\) indica dónde corta el eje y
Pendiente e intersección
\( \large a\) se llama la pendiente:
- Si \( \large a > 0\) la línea es creciente de izquierda a derecha
- Si \( \large a < 0\) la línea es decreciente de izquierda a derecha
- Si \( \large a = 0\) la línea es horizontal, porque sin importar cuál sea \(\large x\), \(\large y\) siempre es el mismo.
\( \large b\) indica que la línea cortará el eje y en el punto \((0,b)\)
Si miramos esta función:
$$ \large y=2x+5 $$
Podemos ver que es una línea creciente, porque \(\large a=2\).
También podemos ver que cortará el eje y en \((0,5)\), porque \(\large b=5\).
Ejemplo
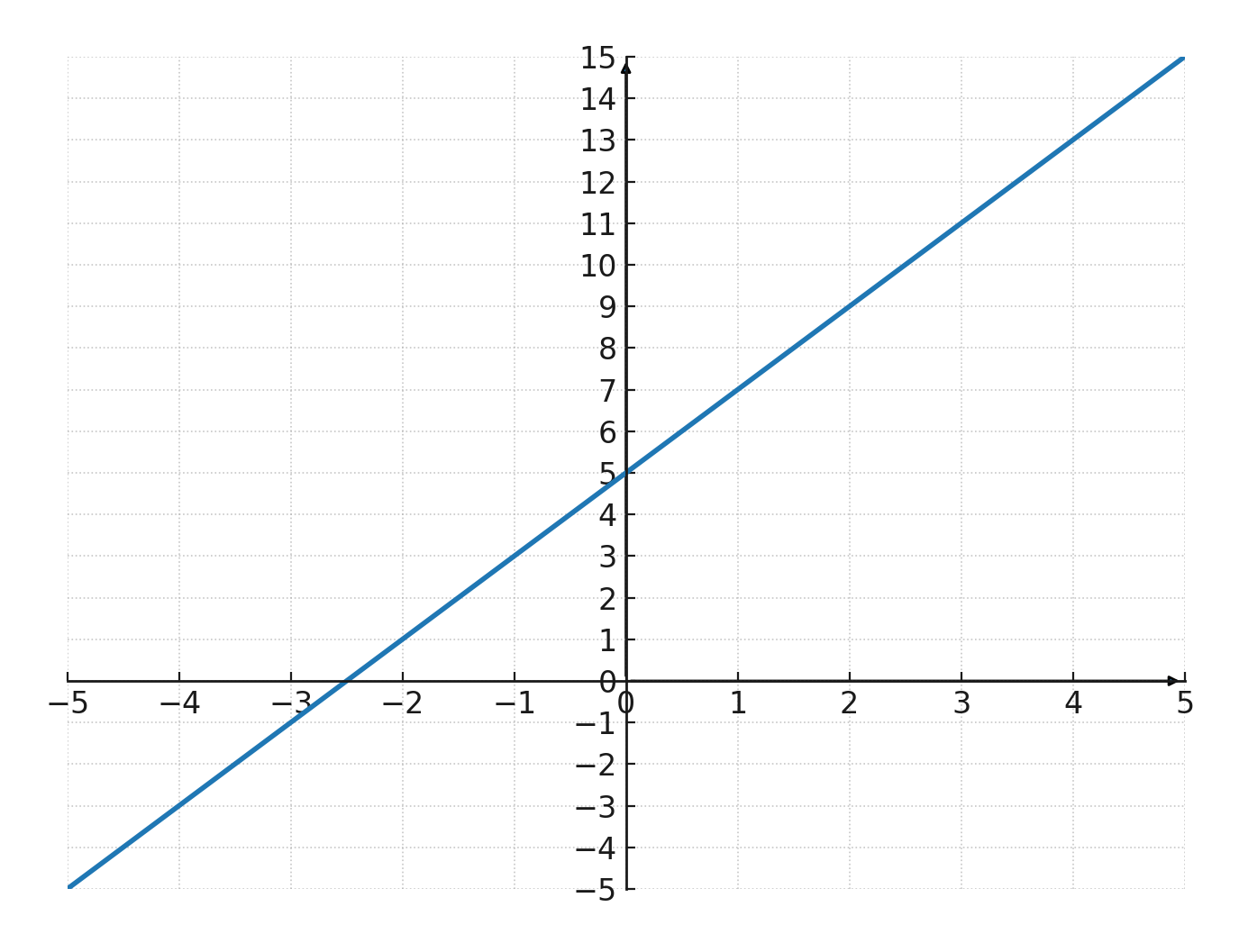
Probamos la función: \( \large y=2x+5 \)
Las coordenadas se colocan en la tabla de valores a continuación y luego en el sistema de coordenadas, para que se pueda dibujar la gráfica:
| \(\large x\) | 1 | 2 | 3 | 4 | 5 |
| \(\large y\) | 7 | 9 | 11 | 13 | 15 |
Encontrar la regla de la función a partir de dos coordenadas
Si tenemos las coordenadas \((2,9)\) y \((4,13)\), es posible encontrar \(\large a\) y \(\large b\) de la siguiente manera:
$$ \large a = \frac{y_2-y_1}{x_2-x_1} \Leftrightarrow $$
$$ \large a = \frac{13-9}{4-2} \Leftrightarrow $$
$$ \large a = \frac{4}{2} \Leftrightarrow $$
$$ \large a = 2 $$
Cuando encontramos \(\large a\), también podemos encontrar \(\large b\) con una de estas dos fórmulas. (No importa cuál se use)
$$ \large b = y_1 - a \cdot x_1 $$
$$ \large b = y_2 - a \cdot x_2 $$
Usamos la primera:
$$ \large b = 9 - 2 \cdot 2 \Leftrightarrow $$
$$ \large b = 9 - 4 \Leftrightarrow $$
$$ \large b = 5 $$
La regla de la función para las coordenadas \((2,9)\) y \((4,13)\) es entonces:
$$ \large y = ax + b $$
$$ \large y = 2x + 5 $$